Question

【题目】已知边长为6的等边中，是高所在直线上的一个动点，连接，将线段绕点顺时针旋转得到，连接，则在点运动的过程中，当线段长度的最小值时，的长度为__________．

Answer 1

【答案】1.5

【解析】

取BA的中点G，连接EG，证明△EBG≌△FBD，根据全等三角形的性质EG=FD，所以只需要求得EG的最短值就好，根据点到直线的距离垂线段最短，当GE⊥AD时，GE最短.此时在Rt△AGE中可求∠BAD=30°，从而根据直角三角形30°角所对边是斜边的一半可求GE=AG=1.5.

解：如图，取BA的中点G，连接EG，

∵△ABC为等边三角形，

∴∠BAC=∠CBA=60°，AB=BC
∵旋转角为60°，
∴∠EBD+∠DBF=60°，
又∵∠EBD+∠EBA=∠CBA=60°，
∴∠DBF=∠ABE，
∵AD是等边△CBA的高，
∴DB=CB，∠BAD=×∠BAC=30°,

∵G为AB的中点

∴BG=AB，
∴DB=BG，
又∵EB旋转到BF，
∴BE=BF，
在△EBG和△FBD中，

，
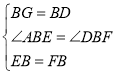∴△EBG≌△FBD（SAS），
∴EG=FD，
根据点到直线的距离，垂线段最短，EG⊥AD时，EG最短，即DF最短，
此时，

∵∠BAD=30°，AG=AB=×6=3，
∴EG=AG=×3=1. 5，
∴DF=1.5，
故答案为：1.5．