Question

【题目】如图，已知：关于x的二次函数的图象与x轴交于点A(1，0)和点B，与y轴交于点C(0，3)，抛物线的对称轴与x轴交于点D.

(1)求二次函数的表达式；

(2)在y轴上是否存在一点P，使△PBC为等腰三角形.若存在，请求出点P的坐标；

(3)有一个点M从点A出发，以每秒1个单位的速度在AB上向点B运动，另一个点N从点D与点M同时出发，以每秒2个单位的速度在抛物线的对称轴上运动，当点M到 达点B时，点M、N同时停止运动，问点M、N运动到何处时，△MNB面积最大，试求出最大面积.

Answer 1

【答案】（1）；（2）存在；（3）1.

【解析】试题分析：（1）把A（1，0）和C（0，3）代入y=x2+bx+c得方程组，解方程组即可得二次函数的表达式；

（2）先求出点B的坐标，再根据勾股定理求得BC的长，当△PBC为等腰三角形时分三种情况进行讨论：①CP=CB；②BP=BC；③PB=PC；分别根据这三种情况求出点P的坐标；

（3）设AM=t则DN=2t，由AB=2，得BM=2﹣t，S△MNB=×（2﹣t）×2t=﹣t2+2t，把解析式化为顶点式，根据二次函数的性质即可得△MNB最大面积；此时点M在D点，点N在对称轴上x轴上方2个单位处或点N在对称轴上x轴下方2个单位处．

试题解析：解：（1）把A（1，0）和C（0，3）代入y=x2+bx+c，

解得：b=﹣4，c=3，

∴二次函数的表达式为：y=x2﹣4x+3；

（2）令y=0，则x2﹣4x+3=0，

解得：x=1或x=3，

∴B（3，0），

∴BC=3，

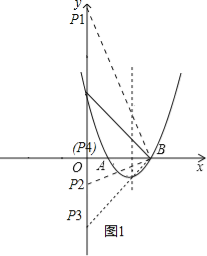
点P在y轴上，当△PBC为等腰三角形时分三种情况进行讨论：如图1，

①当CP=CB时，PC=3，∴OP=OC+PC=3+3或OP=PC﹣OC=3﹣3

∴P1（0，3+3），P2（0，3﹣3）；

②当PB=PC时，OP=OB=3，

∴P3（﹣3，0）；

③当BP=BC时，

∵OC=OB=3

∴此时P与O重合，

∴P4（0，0）；

综上所述，点P的坐标为：（0，3+3）或（0，3﹣3）或（﹣3，0）或（0，0）；

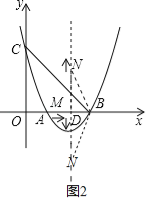
（3）如图2，设AM=t，由AB=2，得BM=2﹣t，则DN=2t，

∴S△MNB=×（2﹣t）×2t=﹣t2+2t=﹣（t﹣1）2+1，

当点M出发1秒到达D点时，△MNB面积最大，最大面积是1．此时点N在对称轴上x轴上方2个单位处或点N在对称轴上x轴下方2个单位处．