题目内容
【题目】如图,已知正方形DEFG的顶点D、E在△ABC的边BC上,顶点G、F分别在边AB、AC上,如果BC=5,△ABC的面积是10,那么这个正方形的边长是_____.

【答案】![]() .
.
【解析】
作AH⊥BC于H,交GF于M,如图,先利用三角形面积公式计算出AH=4,设正方形DEFG的边长为x,则GF=x,MH=x,AM=4-x,再证明△AGF∽△ABC,则根据相似三角形的性质得方程,然后解关于x的方程即可.
解:如图,作AH⊥BC于H,交GF于M,
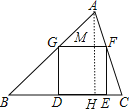
∵△ABC的面积是10,
∴![]() BCAH=10,
BCAH=10,
∴AH=4,
设正方形DEFG的边长为x,则GF=x,MH=x,AM=4-x,
∵GF∥BC,
∴△AGF∽△ABC,
∴![]() ,
,
![]() ,解得x=
,解得x=![]() 。
。
故答案为:![]() 。
。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目