题目内容
【题目】如图,![]() 是☉O的直径,点
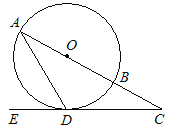
是☉O的直径,点![]() 在☉O上,过点C的切线与AB的延长线交于点P,连接AC,过点O作OD⊥AC交☉O于点D,连接CD.若∠A=30°,PC=6,则CD的长为
在☉O上,过点C的切线与AB的延长线交于点P,连接AC,过点O作OD⊥AC交☉O于点D,连接CD.若∠A=30°,PC=6,则CD的长为 ![]()
![]()

A. ![]() B.
B. ![]() C. 3D.
C. 3D. ![]()
【答案】D
【解析】
连接OC,在Rt△POC中,根据∠P=30°,PC=6,求出OC,进而得出△DCO是等边三角形后解答即可.
解:连接OC,
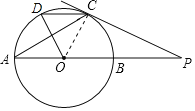
∵OA=OC,∠A=30°,
∴∠OCA=∠A=30°,
∴∠COB=∠A+∠ACO=60°,
∵PC是⊙O切线,
∴∠PCO=90°,∠P=30°,
∵PC=6,
∴OC=PCtan30°=2![]() ,
,
∵OD⊥AC,
∴∠AOD=60°,
∵∠COB=60°,
∴∠DOC=60°,
∵OD=OC,
∴△DOC是等边三角形,
∴CD=OC=2![]() ,
,
故选:D.

练习册系列答案
 课课优能力培优100分系列答案
课课优能力培优100分系列答案 优百分课时互动系列答案
优百分课时互动系列答案
相关题目