题目内容
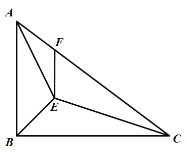
【题目】如图,![]() 为矩形
为矩形![]() 边
边![]() 上一点,连接
上一点,连接![]() ,将
,将![]() 沿
沿![]() 翻折得到
翻折得到![]() ,过点
,过点![]() 作FG⊥BC于点G,若AB=4,FG=1,则AE的长度为____.
作FG⊥BC于点G,若AB=4,FG=1,则AE的长度为____.

【答案】![]()
【解析】
过点E作EM⊥BC于点M,过F作FN⊥EM于点N. 设AE=x,分别解RT△BFG和RT△EFN可得AE的长.
解:如图,过点E作EM⊥BC于点M,过F作FN⊥EM于点N.

则有四边形MGFN、ABME是矩形,NF=MG.MN=FG=1,BM=AE.设AE=x,由翻折的性质知BF=AB=4,
在RT△BFG中,BF=4,FG=1,由勾股定理得BG=![]() ,
,
在RT△EFN中,EN=ME-MN=4-1=3,FN=MG=BG-BM=![]() -X,EF=AE=x.
-X,EF=AE=x.
由勾股定理得方程:![]()
解得x=![]()
所以AE的长度为![]()
故答案为:![]()

练习册系列答案
 新思维假期作业暑假吉林大学出版社系列答案
新思维假期作业暑假吉林大学出版社系列答案 蓝天教育暑假优化学习系列答案
蓝天教育暑假优化学习系列答案
相关题目