Question

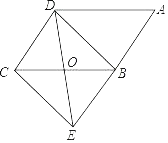
【题目】如图，在ABCD，点O是边BC的中点，连接DO并延长，交AB的延长线于点E，连接BD、EC．

（1）求证：四边形BECD是平行四边形；

（2）若∠BOD＝100°，则当∠A＝　 　时，四边形BECD是矩形．

Answer 1

【答案】(1)证明见解析；(2)50°.

【解析】

(1)由AAS证明△BOE≌△COD，得出OE＝OD，即可得出结论；

(2)由平行四边形的性质得出∠BCD＝∠A＝50°，由三角形的外角性质求出∠ODC＝∠BCD，得出OC＝OD，证出DE＝BC，即可得出结论．

(1)证明：∵四边形ABCD为平行四边形，

∴AB∥DC，AB＝CD，

∴∠OEB＝∠ODC，

又∵O为BC的中点，

∴BO＝CO，

在△BOE和△COD中，

，

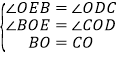∴△BOE≌△COD(AAS)；

∴OE＝OD，

∴四边形BECD是平行四边形；

(2)解：若∠BOD＝100°，则当∠A＝50°时，四边形BECD是矩形．理由如下：

∵四边形ABCD是平行四边形，

∴∠BCD＝∠A＝50°，

∵∠BOD＝∠BCD+∠ODC，

∴∠ODC＝100°﹣50°＝50°＝∠BCD，

∴OC＝OD，

∵BO＝CO，OD＝OE，

∴DE＝BC，

∵四边形BECD是平行四边形，

∴四边形BECD是矩形；

故答案是：50°．