题目内容
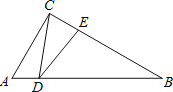
【题目】如图,⊙O是△ABC的外接圆,AB是直径,过点O作OD⊥CB,垂足为点D,延长DO交⊙O于点E,过点E作PE⊥AB,垂足为点P,作射线DP交CA的延长线于F点,连接EF,
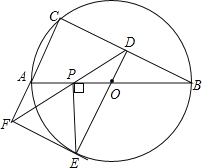
(1)求证:OD=OP;(2)求证:FE是⊙O的切线.
【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题(2)证明△POE≌△ADO可得DO=EO;
(3)连接AE,BE,证出△APE≌△AFE即可得出结论.
试题解析:(1)∵∠EPO=∠BDO=90° ∠EOP=∠BOD
OE=OB
∴△OPE≌△ODB
∴OD="OP"
(2)连接EA,EB
∴∠1=∠EBC
∵AB是直径
∴∠AEB=∠C=90°
∴∠2+∠3=90°
∵∠3=∠DEB
∵∠BDE=90°
∴∠EBC+∠DEB=90°
∴∠2=∠EBC=∠1
∵∠C=90° ∠BDE=90°
∴CF∥OE
∴∠ODP=∠AFP
∵OD=OP
∴∠ODP=∠OPD
∵∠OPD=∠APF
∴∠AFP=∠APF
∴AF=AP 又AE=AE
∴△APE≌△AFE
∴∠AFE=∠APE=90°
∴∠FED=90°
∴FE是⊙O的切线

练习册系列答案
相关题目