��Ŀ����
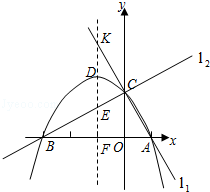
����Ŀ����ͼ��������A���ʾ��![]() ��B���ʾ��
��B���ʾ��![]() ����
����![]() ��
��![]() ����
����![]() ��
��
![]()
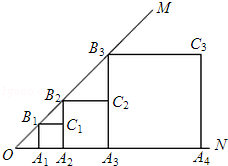
��1����A��ʾ����Ϊ_______����B��ʾ����Ϊ__________;
��2������A���C֮��ľ����ʾΪAC����B���C֮��ľ����ʾΪBC��������������һ��C��ʹAC��3BC����C���ʾ����__________;
��3������ԭ��O����һ���壬һС��״ӵ�A����1����λ/����ٶ������˶���ͬʱ��һС���Ҵӵ�B����2����λ/����ٶ�Ҳ�����˶������������������Ĵ�С���ɿ���һ�㣩��ԭ�����ٶ����෴�ķ����˶������˶���ʱ��Ϊt���룩����ֱ��ʾ���ס�����С��ԭ��ľ��루�ú�t�Ĵ���ʽ��ʾ��
���𰸡���1��-5��7��2��4��13����3���ף�5+t���ң�0t3.5ʱ��72t����t>3.5ʱ��2t7
�������������������1�����ݷǸ����������з������a��b��ֵ���Ӷ��ý⣻��2��������������ı�ʾ�г�����ֵ���̣�Ȼ����⼴�ɣ���3����С����������ϵ����������ʾ���ɣ���С��������������ƶ��������ֱַ���ʽ��ʾ���ɣ�
���������(1)������ã�a+5=0��b7=0��
���a=5��b=7��
���ԣ���A��ʾ5����B��ʾ7��
(2)���C��ʾx��������ã�|5x|=3|7x|��
����,5+x=3(7x)��5+x=3(7x)��
���x=4����x=13��
���ԣ���C��ʾ����Ϊ4��13��
(3)�ף���С��״ӵ�A����1����λ/����ٶ������˶���
���ԭ��ľ���Ϊ|5t|=5+t��
��С���Ҵӵ�B����2����λ/����ٶ�Ҳ�����˶���
���ҵ���ԭ���ʱ��Ϊ7��2=3.5��
�൱0t3.5ʱ��С��ԭ��ľ���Ϊ72t��
��t>3.5ʱС��ԭ��ľ���Ϊ2t7.

����Ŀ��ij��Ϊ�˹��������Լ��ˮ�����÷ֽμƷѵķ������¼���ÿ����ͥ��ˮ�ѣ�����ˮ��������20m3ʱ����2Ԫ/m3���㣻����ˮ������20m3ʱ�����е�20m3��2Ԫ/m3���㣬�������ְ�2.6Ԫ/m3���㣮��ij����ͥ����ˮ��xm3��
�·� | 4�� | 5�� | 6�� |
��ˮ�� | 15 | 17 | 21 |
��1���ú�x��ʽ�ӱ�ʾ��
��0��x��20ʱ��ˮ��Ϊ�� ��Ԫ��
��x��20ʱ��ˮ��Ϊ�� ��Ԫ��
��2��С���ҵڶ�������ˮ������ϱ���С����������ȹ�����ˮ�Ѷ���Ԫ��