Question

【题目】已知，如图，∠MON=45°，OA1=1，作正方形A1B1C1A2 ， 周长记作C1；再作第二个正方形A2B2C2A3 ， 周长记作C2；继续作第三个正方形A3B3C3A4 ， 周长记作C3；点A1、A2、A3、A4…在射线ON上，点B1、B2、B3、B4…在射线OM上，…依此类推，则第n个正方形的周长Cn= ．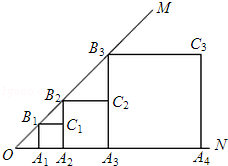

Answer 1

【答案】2n+1
【解析】解：∵∠MON=45°， ∴△OA1B1是等腰直角三角形，
∵OA1=1，
∴正方形A1B1C1A2的边长为1，
∵B1C1∥OA2 ，
∴∠B2B1C1=∠MON=45°，
∴△B1C1B2是等腰直角三角形，
∴正方形A2B2C2A3的边长为：1+1=2，
同理，第3个正方形A3B3C3A4的边长为：2+2=22 ， 其周长为：4×22=24 ，
第4个正方形A4B4C4A5的边长为：4+4=23 ， 其周长为：4×23=25 ，
第5个正方形A5B5C5A6的边长为：8+8=24 ， 其周长为：4×24=26 ，
则第n个正方形的周长Cn=2n+1 ．
故答案为：2n+1 ．
判断出△OA1B1是等腰直角三角形，求出第一个正方形A1B1C1A2的边长为1，再求出△B1C1B2是等腰直角三角形，再求出第2个正方形A2B2C2A3的边长为2，然后依次求出第3个正方形的边长，第4个正方形的边长第5个正方形的边长，即可得出周长的变化规律．