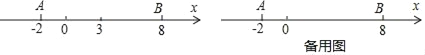Question

【题目】已知两直线l1 ， l2分别经过点A（1，0），点B（﹣3，0），并且当两直线同时相交于y正半轴的点C时，恰好有l1⊥l2 ， 经过点A、B、C的抛物线的对称轴与直线l1交于点K，如图所示．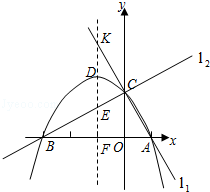

（1）求点C的坐标，并求出抛物线的函数解析式；
（2）抛物线的对称轴被直线l1 ， 抛物线，直线l2和x轴依次截得三条线段，问这三条线段有何数量关系？请说明理由；
（3）当直线l2绕点C旋转时，与抛物线的另一个交点为M，请找出使△MCK为等腰三角形的点M，简述理由，并写出点M的坐标．

Answer 1

【答案】
（1）

解：解法1：∵l1⊥l2，

∴∠ACB=90°，即∠ACO+∠BCO=90°，

又∠ACO+∠CAO=90°，

∴∠BCO=∠CAO，又∠COA=∠BOC=90°

∴△BOC∽△COA，

∴ ，

即 ，

∴ ，

∴点C的坐标是（0， ），

由题意，可设抛物线的函数解析式为 ，

把A（1，0），B（﹣3，0）的坐标分别代入 ，

得 ，

解这个方程组，得 ，

∴抛物线的函数解析式为 ．

解法2：由勾股定理，得（OC2+OB2）+（OC2+OA2）=BC2+AC2=AB2，

又∵OB=3，OA=1，AB=4，

∴ ，

∴点C的坐标是（0， ），

由题意可设抛物线的函数解析式为y=a（x﹣1）（x+3），把C（0， ）代入

函数解析式得 ，

所以，抛物线的函数解析式为 =

（2）

解：解法1：截得三条线段的数量关系为KD=DE=EF．

理由如下：

设直线l1的解析式为y=kx+b，把A（1，0），C（0， ），代入解析式，

解得k=﹣ ，b= ，

所以直线l1的解析式为 ，

同理可得直线l2的解析式为 ，

抛物线的对称轴为直线x=﹣1，

由此可求得点K的坐标为（﹣1， ），

点D的坐标为（﹣1， ），点E的坐标为（﹣1， ），点F的坐标为（﹣1，0），

∴KD= ，DE= ，EF= ，

∴KD=DE=EF．

解法2：截得三条线段的数量关系为KD=DE=EF，

理由如下：

由题意可知Rt△ABC中，∠ABC=30°，∠CAB=60°，

则可得 ， ，

由顶点D坐标（﹣1， ）得 ，

∴KD=DE=EF=

（3）

解：当点M的坐标分别为（﹣2， ），（﹣1， ）时，△MCK为等腰三角形．

理由如下：

（i）连接BK，交抛物线于点G，

∵F（﹣1，0），直线l1的解析式为 ，

∴K（﹣1，2 ），

∵B（﹣3，0），

∴直线BK的解析式为：y= x+3 ①，

∵抛物线的函数解析式为y═ ②；

①②联立即可求出点G的坐标为（﹣2， ），

又∵点C的坐标为（0， ），则GC∥AB，

∵可求得AB=BK=4，且∠ABK=60°，即△ABK为正三角形，

∴△CGK为正三角形

∴当l2与抛物线交于点G，即l2∥AB时，符合题意，此时点M1的坐标为（﹣2， ），（ii）连接CD，由KD= ，CK=CG=2，∠CKD=30°，易知△KDC为等腰三角形，

∴当l2过抛物线顶点D时，符合题意，此时点M2坐标为（﹣1， ），（iii）当点M在抛物线对称轴右边时，只有点M与点A重合时，满足CM=CK，

但点A、C、K在同一直线上，不能构成三角形，

综上所述，当点M的坐标分别为（﹣2， ），（﹣1， ）时，△MCK为等腰三角形．

【解析】（1）利用△BOC∽△COA，得出C点坐标，再利用待定系数法求出二次函数解析式即可；（2）可求得直线l1的解析式为 ，直线l2的解析式为 ，进而得出D，E，F点的坐标即可得出，三条线段数量关系；（3）利用等边三角形的判定方法得出△ABK为正三角形，以及易知△KDC为等腰三角形，进而得出△MCK为等腰三角形时M点坐标．