题目内容
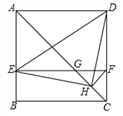
【题目】如图,在正方形ABCD中,AC为对角线,E为AB上一点,过点E作![]() ,与AC、DC分别交于点
,与AC、DC分别交于点![]() 为CG的中点,连结DE、EH、DH、
为CG的中点,连结DE、EH、DH、![]() 下列结论:
下列结论: ![]() ;
; ![]() ≌
≌![]() ;
; ![]() ;
; ![]() 若
若![]() ,则
,则![]() 其中结论正确的有
其中结论正确的有![]()
A. 1个 B. 2个 C. 3个 D. 4个
【答案】D
【解析】试题解析:①∵四边形ABCD为正方形,EF∥AD,
∴EF=AD=CD,∠ACD=45°,∠GFC=90°,
∴△CFG为等腰直角三角形,
∴GF=FC,
∵EG=EF-GF,DF=CD-FC,
∴EG=DF,故①正确;
②∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=CH,∠GFH=![]() ∠GFC=45°=∠HCD,
∠GFC=45°=∠HCD,
在△EHF和△DHC中, ,
,
∴△EHF≌△DHC(SAS),故②正确;
③∵△EHF≌△DHC(已证),
∴∠HEF=∠HDC,
∴∠AEH+∠ADH=∠AEF+∠HEF+∠ADF-∠HDC=∠AEF+∠ADF=180°,故③正确;
④∵![]() ,
,
∴AE=2BE,
∵△CFG为等腰直角三角形,H为CG的中点,
∴FH=GH,∠FHG=90°,
∵∠EGH=∠FHG+∠HFG=90°+∠HFG=∠HFD,
在△EGH和△DFH中, ,
,
∴△EGH≌△DFH(SAS),
∴∠EHG=∠DHF,EH=DH,∠DHE=∠EHG+∠DHG=∠DHF+∠DHG=∠FHG=90°,
∴△EHD为等腰直角三角形,
如图,过H点作HM⊥CD于M,
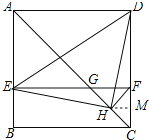
设HM=x,则DM=5x,DH=![]() x,CD=6x,
x,CD=6x,
则S△DHC=![]() ×HM×CD=3x2,S△EDH=
×HM×CD=3x2,S△EDH=![]() ×DH2=13x2,
×DH2=13x2,
∴3S△EDH=13S△DHC,故④正确;
故选D.

 品学双优卷系列答案
品学双优卷系列答案 小学期末冲刺100分系列答案
小学期末冲刺100分系列答案 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案【题目】某校九年级为了解学生课堂发言情况,随机抽取该年级部分学生,对他们某天在课堂上发言的次数进行了统计,其结果如下表,并绘制了如图所示的两幅不完整的统计图,已知B、E两组发言人数的比为5:2,
组别 | 课堂发言次数n |
A | 0≤n<3 |
B | 3≤n<6 |
C | 6≤n<9 |
D | 9≤n<12 |
E | 12≤n<15 |
F | 15≤n<18 |
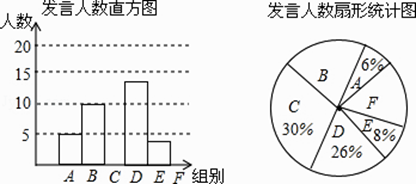
请结合图中相关数据回答下列问题:
(1)样本容量是 , 并补全直方图;
(2)该年级共有学生800人,请估计该年级在这天里发言次数不少于12次的人数;
(3)已知A组发言的学生中恰好有1位女生,E组发言的学生中有2位男生,现从A组与E组中分别抽一位学生写报告,请用列表法或画树状图的方法,求所抽的两位学生恰好都是男生的概率.