题目内容
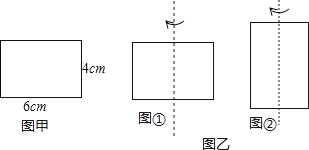
【题目】探究:有一长6cm,宽4cm的矩形纸板,现要求以其一组对边中点所在直线为轴,旋转180°,得到一个圆柱,现可按照两种方案进行操作:
方案一:以较长的一组对边中点所在直线为轴旋转,如图①;
方案二:以较短的一组对边中点所在直线为轴旋转,如图②.
(1)请通过计算说明哪种方法构造的圆柱体积大;
(2)如果该矩形的长宽分别是5cm和3cm呢?请通过计算说明哪种方法构造的圆柱体积大;
(3)通过以上探究,你发现对于同一个矩形(不包括正方形),以其一组对边中点所在直线为轴旋转得到一个圆柱,怎样操作所得到的圆柱体积大(不必说明原因)?
【答案】(1)方案一构造的圆柱的体积大;(2)方案一构造的圆柱的体积大;(3)以较长一组对边中点所在直线为轴旋转得到的圆柱的体积大.
【解析】
(1)和(2)均可分别计算两种旋转方式所得圆柱的体积并进行比较即可;
(3)根据上述两问的计算结果确定即可.
(1)方案一:π×32×4=36π(cm3),
方案二:π×22×6=24π(cm3),
∵36π>24π,
∴方案一构造的圆柱的体积大;
(2)方案一:π×(![]() )2×3=
)2×3=![]() π(cm3),
π(cm3),
方案二:π×(![]() )2×5=
)2×5=![]() π(cm3),
π(cm3),
∵![]() π>
π>![]() π,
π,
∴方案一构造的圆柱的体积大;
(3)由(1)、(2)得,以较长一组对边中点所在直线为轴旋转得到的圆柱的体积大.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目