��Ŀ����
����Ŀ����ͼ1��������y=ax2+b�Ķ�������Ϊ��0����1�����Ҿ�����A����2��0���� 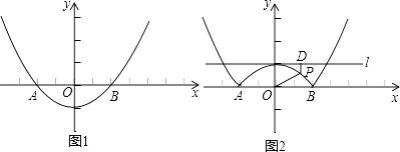
��1���������ߵĽ���ʽ��
��2������������y=ax2+b����x���·���ͼ����x�ᷭ�۵�x���Ϸ���x���Ϸ���ͼ�ֲ��䣬�͵õ��˺���y=|ax2+b|ͼ���ϵ�����һ��P��ֱ��l�Ǿ�����0��1����ƽ����x���ֱ�ߣ�����P��ֱ��l�Ĵ��ߣ�����ΪD�����벢̽����PO��PD�IJ��Ƿ�Ϊ��ֵ������ǣ�������˶�ֵ��������ǣ���˵�����ɣ� ��ע���ڽ�������У��������������ѣ������Ķ�����IJ��ϣ�
���Ķ����ϣ�
�� ��ƽ��ֱ������ϵ�У���A��B���������ֱ�ΪA��x1 �� y1����B��x2 �� y2������A��B�����ľ���Ϊ|AB|= ![]() �������ʽ���������빫ʽ��
�������ʽ���������빫ʽ��
���磺��֪A��B���������ֱ�Ϊ����1��2������2����2������A��B�����ľ���Ϊ|AB|= ![]() =5��
=5��
�� ��ʽ�ֽ⣺x4+2x2y2+y4=��x2+y2��2 ��
���𰸡�
��1���⣺���������������߽���ʽΪy=ax2��1��
����A����2��0�����룬�ã�4a��1=0��
��ã�a= ![]() ��
��
�������ߵĽ���ʽΪy= ![]() x2��1
x2��1
��2���⣺��ͼ��
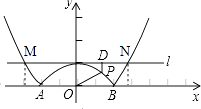
�������⣬����2��x��2ʱ��y=�� ![]() x2+1��
x2+1��
��x����2��x��2ʱ��y= ![]() x2��1��
x2��1��
�� 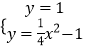 �ɵõ�M����2
�ɵõ�M����2 ![]() ��1������N��2
��1������N��2 ![]() ��1����
��1����
�� ����2��x��2ʱ�����P����Ϊ��a���� ![]() a2+1����
a2+1����
��PO��PD= ![]() ��[1������
��[1������ ![]() a2+1��]
a2+1��]
= ![]() a2+1��
a2+1�� ![]() a2
a2
=1��
�ڵ���2 ![]() ��x����2��2
��x����2��2 ![]() ʱ�����P������Ϊ��a��
ʱ�����P������Ϊ��a�� ![]() a2��1����
a2��1����
��PO��PD= ![]() ��[1����
��[1���� ![]() a2��1��]
a2��1��]
= ![]() a2+1��2+
a2+1��2+ ![]() a2
a2
= ![]() a2��1��
a2��1��
�۵�x����2 ![]() ��x��2
��x��2 ![]() ʱ�����P������Ϊ��a��
ʱ�����P������Ϊ��a�� ![]() a2��1����
a2��1����
��PO��PD= ![]() ��[��
��[�� ![]() a2��1����1]
a2��1����1]
= ![]() a2+1��
a2+1�� ![]() a2+2
a2+2
=3��
���ϣ���x����2 ![]() ����2��x��2��x��2
����2��x��2��x��2 ![]() ʱ��PO��PD�IJ�Ϊ��ֵ
ʱ��PO��PD�IJ�Ϊ��ֵ
����������1������ϵ�������ɵã���2���ȸ��������ʾ�����ۺ������߽���ʽ�������y=1ʱx��ֵ���̶��ɷ֩�2��x��2����2 ![]() ��x����2��2
��x����2��2 ![]() ��x����2
��x����2 ![]() ��x��2
��x��2 ![]() ��������������������빫ʽ��ʽ��ʾ��PO��PD�IJ�ɵó��𰸣�
��������������������빫ʽ��ʽ��ʾ��PO��PD�IJ�ɵó��𰸣�
�����㾫����������Ŀ����֪���������ö��κ���ͼ���Լ�ϵ��a��b��c�Ĺ�ϵ��������ͼ�α仯-�ԳƵ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ���ն��κ���y=ax2+bx+c�У�a��b��c�ĺ��壺a��ʾ���ڷ���a>0ʱ�������߿�������; a<0ʱ�������߿�������b��Գ����йأ��Գ���Ϊx=-b/2a;c��ʾ��������y��Ľ������꣺��0��c��������x��ԳƵĵ�����������������x��Գ�ʱ�����ǵ������У�x��ȣ�y�ķ����෴������P��x��y������x��ĶԳƵ�ΪP����x��-y��������y��ԳƵĵ�����������������y��Գ�ʱ�����ǵ������У�y��ȣ�x�ķ����෴������P��x��y������y��ĶԳƵ�ΪP����-x��y����

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�����Ŀ��.ij����ʵʩ������ˮ�����ǰ���Ծ���������ˮ��������˵��飬�±���ͨ�������������õ�50����ͥȥ����ƽ����ˮ��![]() ��λ����
��λ����![]() �������������ݽ�������������
�������������ݽ�������������

Ƶ���ֲ���
���� | ���� | Ƶ�� |
| ���� | 11 |
|
| 19 |
| ||
�ϼ� |
| 2 50 |
![]() ������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
������Ƶ���ֲ�����Ƶ���ֲ�ֱ��ͼ����������
![]() ��ֱ��ͼ�����ܵõ�ʲô��Ϣ��
��ֱ��ͼ�����ܵõ�ʲô��Ϣ�� ![]() д����������
���������![]() ��
��
![]() Ϊ�˹�����Լ��ˮ��Ҫȷ��һ����ˮ���ı�������������IJ��ְ�
Ϊ�˹�����Լ��ˮ��Ҫȷ��һ����ˮ���ı�������������IJ��ְ�![]() ���۸��շѣ���Ҫʹ
���۸��շѣ���Ҫʹ![]() �ļ�ͥ�շѲ���Ӱ�죬����ü�ͥ�¾���ˮ��Ӧ�ö�Ϊ���٣�Ϊʲô��
�ļ�ͥ�շѲ���Ӱ�죬����ü�ͥ�¾���ˮ��Ӧ�ö�Ϊ���٣�Ϊʲô��