题目内容
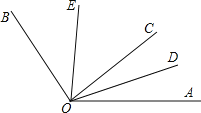
【题目】如图,∠AOB=120°,OC是∠AOB内部任意一条射线,OD、OE分别是∠AOC、∠BOC的角平分线,下列叙述正确的是( )
A. ∠DOE的度数不能确定 B. ∠AOD=![]() ∠EOC
∠EOC
C. ∠AOD+∠BOE=60° D. ∠BOE=2∠COD
【答案】C
【解析】
A.∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠DOE=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=60°
∠AOB=60°
故本选项叙述错误;
B.∵OD是∠AOC的角平分线,
∴∠AOD=![]() ∠AOC.
∠AOC.
又∵OC是∠AOB内部任意一条射线,
∴∠AOC=∠EOC不一定成立。
故本选项叙述错误;
C.∵OD、OE分别是∠AOC、∠BOC的平分线,
∴∠BOE+∠AOD=∠EOC+∠DOC=∠DOE=![]() (∠BOC+∠AOC)=
(∠BOC+∠AOC)=![]() ∠AOB=60°
∠AOB=60°
故本选项叙述正确;
D.∵OC是∠AOB内部任意一条射线,
∴∠BOE=∠AOC不一定成立,
∴∠BOE=2∠COD不一定成立。
故本选项叙述错误;
故选:C.

练习册系列答案
相关题目