题目内容
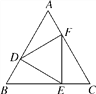
【题目】如图,AB是⊙O的直径,OD垂直弦AC于点E,且交⊙O于点D,过点D作⊙O的切线与BA的延长线相交于点F,下列结论不一定正确的是( ) 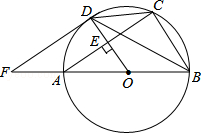
A.∠CDB=∠BFD
B.△BAC∽△OFD
C.DF∥AC
D.OD=BC
【答案】D
【解析】解:∵AD是切线, ∴OD⊥DF,∵AC⊥OD,
∴DF∥AC,故C正确,
∴∠F=∠CAB,
∵∠CDB=∠CBA,
∴∠CDB=∠BFD,故A正确,
∵AB是直径,
∴∠AEO=∠ACB=90°,
∴OE∥BC,
∴△BAC∽△OAE,∵△OAE∽△OFD,
∴△BAC∽△OFD,故B正确,
无法证明OD=BC,
故选D.
【考点精析】掌握切线的性质定理和相似三角形的判定是解答本题的根本,需要知道切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径;相似三角形的判定方法:两角对应相等,两三角形相似(ASA);直角三角形被斜边上的高分成的两个直角三角形和原三角形相似; 两边对应成比例且夹角相等,两三角形相似(SAS);三边对应成比例,两三角形相似(SSS).

【题目】节能电动车越来越受到人们的喜欢,新开发的各种品牌电动车相继投入市场.小李车行经营的A型节能电动车2015年销售总额为m万元,2016年每辆A型节能电动车的销售价比2015年降低2000年,若2015年和2016年卖出的节能电动车的数量相同(同一型号的节能电动车每辆的销售价格相同),则2016年的销售总额比2015年减少20%.
(1)2016年A型节能电动车每辆售价多少万元?(用列方程方法解答)
(2)小李车行计划端午节后新购进一批A型节能电动车和新型B型节能电动车,每购进3辆节能电动车,批发商就给车行返回1500元.若新款B型节能电动车的进货数量是A型节能电动车的进货数量的2倍,全部销售获得的利润不少于18万元,且2016年A,B两种型号节能电动车的进货和销售价格如表,那么2016年新款B型节能电动车至少要购进多少辆?
A型节能电动车 | B型节能电动车 | |
进货价格(万元/辆) | 0.55 | 0.7 |
销售价格(万元/辆) | 2016年的销售价格 | 2 |