Question

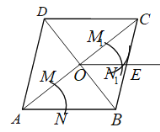
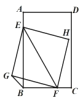
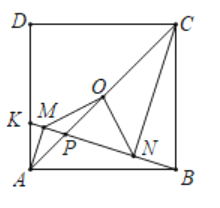
【题目】如图，边长为1的正方形ABCD中，点K在AD上，连接BK，过点A，C作BK的垂线，垂足分别为M，N，点O是正方形ABCD的中心，连接OM，ON．

（1）求证：AM=BN；

（2）请判断△OMN的形状，并说明理由；

（3）若点K在线段AD上运动（不包括端点），设AK=x，△OMN的面积为y，求y关于x的函数关系式（写出x的范围）；若点K在射线AD上运动，且△OMN的面积为，请直接写出AK长．

Answer 1

【答案】（1）详见解析；（2）是等腰直角三角形，理由详见解析；（3），长为或3．

【解析】

（1）由“AAS”可证△ABM≌△BCN，可得AM＝BN；

（2）连接OB，由“SAS”可证△AOM≌△BON，可得MO＝NO，∠AOM＝∠BON，由余角的性质可得∠MON＝90°，可得结论；

（3）由勾股定理可求BK的值，由，四边形ABCD是正方形，可得：，，则可求得，由三角形面积公式可求得；点K在射线AD上运动，分两种情况：当点K在线段AD上时和当点K在线段AD的延长线时分别求解即可得到结果．

解：（1）证明：

∵

∴

又∵

∴

∴

又

∴≌（AAS）

∴

（2）是等腰直角三角形

理由如下：连接，

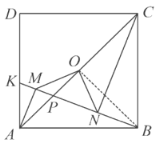
∵为正方形的中心

∴OA＝OB，∠OBA＝∠OAB＝45°＝∠OBC，AO⊥BO，

∵∠MAB＝∠CBM，

∴，即

∵

∴≌（SAS）

∴，

∵

∵∠AON+∠BON＝90°，

∴∠AON+∠AOM＝90°，

∴

∴是等腰直角三角形．

（3）在中，

由，四边形ABCD是正方形，

可得：，

∴，

∴，得：

∴，得：

∴

∴

即：

当点K在线段AD上时，则，

解得：x1＝3（不合题意舍去），，

当点K在线段AD的延长线时，同理可求得

∴，

解得：x1＝3，（不合题意舍去），

综上所述：长为或3时，△OMN的面积为．