题目内容
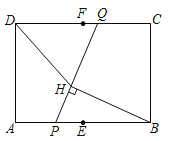
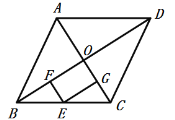
【题目】如图,面积为S的菱形ABCD中,点O为对角线的交点,点E是线段BC单位中点,过点E作EF⊥BD于F,EG⊥AC与G,则四边形EFOG的面积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】B
【解析】
由菱形的性质得出OA=OC,OB=OD,AC⊥BD,S=![]() AC×BD,证出四边形EFOG是矩形,EF∥OC,EG∥OB,得出EF、EG都是△OBC的中位线,则EF=
AC×BD,证出四边形EFOG是矩形,EF∥OC,EG∥OB,得出EF、EG都是△OBC的中位线,则EF=![]() OC=
OC=![]() AC,EG=
AC,EG=![]() OB=
OB=![]() BD,由矩形面积即可得出答案.
BD,由矩形面积即可得出答案.
解:∵四边形ABCD是菱形,
∴OA=OC,OB=OD,AC⊥BD,S=![]() AC×BD,
AC×BD,
∵EF⊥BD于F,EG⊥AC于G,
∴四边形EFOG是矩形,EF∥OC,EG∥OB,
∵点E是线段BC的中点,
∴EF、EG都是△OBC的中位线,
∴EF=![]() OC=
OC=![]() AC,EG=
AC,EG=![]() OB=
OB=![]() BD,
BD,
∴矩形EFOG的面积=EF×EG=![]() AC×
AC×![]() BD=
BD=![]()
![]() =
=![]() S;
S;
故选:B.

练习册系列答案
相关题目
【题目】为了传承中华优秀传统文化,某校组织了一次全校![]() 名学生参加的“汉字听写”大赛,并设成绩优胜奖.赛后发现所有参赛学生的成绩不低于
名学生参加的“汉字听写”大赛,并设成绩优胜奖.赛后发现所有参赛学生的成绩不低于![]() 分,为了更好的了解本次大赛的成绩分布情况,随机抽取了
分,为了更好的了解本次大赛的成绩分布情况,随机抽取了![]() 名学生的成绩(成绩
名学生的成绩(成绩![]() 取整数,总分
取整数,总分![]() 分)作为样本进行整理,得到下列不完整的统计图表:
分)作为样本进行整理,得到下列不完整的统计图表:
成绩在这![]() 组的数据是:
组的数据是:
![]()
![]()
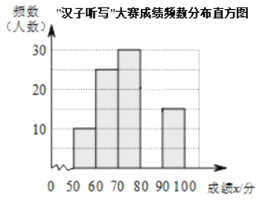
“汉字听写”大赛成绩段频数频率统计表
成绩 | 频数 | 频率 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
根据以上信息,解答下列问题:
(1)表中![]() ,
,![]() ;
;
(2)请补全频数分布直方图;
(3)这次比赛成绩的中位数是 ;
(4)若这次比赛成绩在![]() 分以上(含
分以上(含![]() 分)的学生获得优胜奖,估计该校参加这次比赛的
分)的学生获得优胜奖,估计该校参加这次比赛的![]() 名学生中获得优胜奖的人数.
名学生中获得优胜奖的人数.