Question

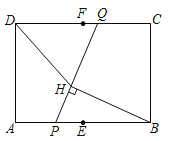
【题目】已知：矩形的边，，点从点出发沿线段向点匀速运动，点同时从点出发沿线段向点匀速运动，速度均为，当一个点到达终点时另一个点也停止运动．连接，以为对角线作正方形，连接，则的长度为____．

Answer 1

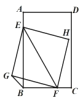
【答案】

【解析】

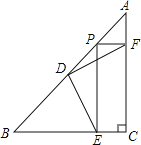
过点G作GN⊥BC交CB的延长线于N，过点E作EM⊥GN，交NG的延长线于M，通过证明点G，点B，点F，点E四点共圆，可得∠GBE=∠GFE=45°，可得GN=BN，通过证明△MEG≌△NGF，可得MG=NF=BF+BN=6-FC+BN，GN=ME，由线段的和差关系可求BN的长，即可求解．

如图，过点G作GN⊥BC交CB的延长线于N，过点E作EM⊥GN，交NG的延长线于M，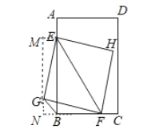

∵点E，点F，速度均为1cm/s，
∴AE=CF，
∵四边形EGFH是正方形，
∴EG=GF，∠EGF=∠ABC=90°，∠EFG=45°，
∴点G，点B，点F，点E四点共圆，
∴∠GBE=∠GFE=45°，
∴∠GBN=45°，
∵GN⊥BC，
∴∠NGB=∠GBN=45°，
∴GN=BN，
∵EM⊥GN，GN⊥BC，∠EBN=90°，
∴四边形EBNM是矩形，
∴BE=MN=8-AE，ME=NB，
∵EM⊥GN，GN⊥BC，
∴∠M=∠N=90°，
∴∠MGE+∠MEG=90°，
又∵∠MGE+∠NGF=90°，
∴∠MEG=∠NGC，
∴△MEG≌△NGF（AAS），
∴MG=NF=BF+BN=6-FC+BN，
GN=ME，
∴MN=MG+GN=6-FC+BN+ME=6-AE+2BN=8-AE，
∴BN=1，
∴GN=BN=1，
∴GB=BN=，

故答案为：．