题目内容
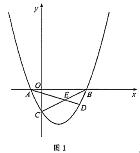
【题目】如图,在![]() 的边
的边![]() 上取一点
上取一点![]() ,以
,以![]() 为圆心,
为圆心,![]() 为半径画⊙O,⊙O与边
为半径画⊙O,⊙O与边![]() 相切于点
相切于点![]() ,
,![]() ,连接
,连接![]() 交⊙O于点
交⊙O于点![]() ,连接
,连接![]() ,并延长交线段
,并延长交线段![]() 于点
于点![]() .
.
(1)求证:![]() 是⊙O的切线;
是⊙O的切线;
(2)若![]() ,
,![]() ,求⊙O的半径;
,求⊙O的半径;
(3)若![]() 是
是![]() 的中点,试探究
的中点,试探究![]() 与
与![]() 的数量关系并说明理由.
的数量关系并说明理由.
【答案】(1)见解析;(2)![]() ;(3)
;(3)![]() ,理由见解析
,理由见解析
【解析】
(1)连接OD,由切线的性质可得∠ADO=90°,由“SSS”可证△ACO≌△ADO,可得∠ADO=∠ACO=90°,可得结论;
(2)由锐角三角函数可设AC=4x,BC=3x,由勾股定理可求BC=6,再由勾股定理可求解;
(3)连接OD,DE,由“SAS”可知△COE≌△DOE,可得∠OCE=∠OED,由三角形内角和定理可得∠DEF=180°-∠OEC-∠OED=180°-2∠OCE,∠DFE=180°-∠BCF-∠CBF=180°-2∠OCE,可得∠DEF=∠DFE,可证DE=DF=CE,可得结论.
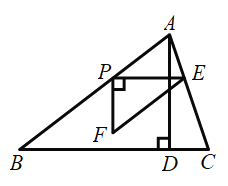
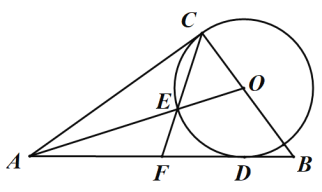
解:(1)如图,连接OD,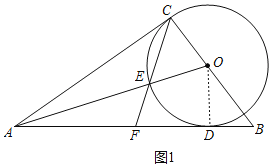
∵⊙O与边AB相切于点D,
∴OD⊥AB,即∠ADO=90°,
∵AO=AO,AC=AD,OC=OD,
∴△ACO≌△ADO(SSS),
∴∠ADO=∠ACO=90°,
又∵OC是半径,
∴AC是⊙O的切线;
(2)在Rt△ABC中,tanB=![]() =
=![]() ,
,
∴设AC=4x,BC=3x,
∵AC2+BC2=AB2,
∴16x2+9x2=100,
∴x=2,
∴BC=6,
∵AC=AD=8,AB=10,
∴BD=2,
∵OB2=OD2+BD2,
∴(6-OC)2=OC2+4,
∴OC=![]() ,
,
故⊙O的半径为![]() ;
;
(3)连接OD,DE,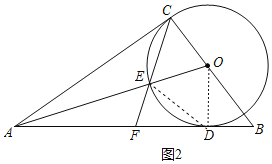
由(1)可知:△ACO≌△ADO,
∴∠ACO=∠ADO=90°,∠AOC=∠AOD,
又∵CO=DO,OE=OE,
∴△COE≌△DOE(SAS),
∴∠OCE=∠ODE,
∵OC=OE=OD,
∴∠OCE=∠OEC=∠OED=∠ODE,
∴∠DEF=180°-∠OEC-∠OED=180°-2∠OCE,
∵点F是AB中点,∠ACB=90°,
∴CF=BF=AF,
∴∠FCB=∠FBC,
∴∠DFE=180°-∠BCF-∠CBF=180°-2∠OCE,
∴∠DEF=∠DFE,
∴DE=DF=CE,
∴AF=BF=DF+BD=CE+BD.

 名校课堂系列答案
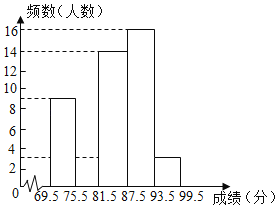
名校课堂系列答案【题目】我市要开展“不忘初心,牢记使命”主题演讲比,某中学将参加本校选拔赛的50名选手的成绩(满分为100分,得分为正整数)分成五组,并绘制了不完整的统计图表.
分数段 | 频数 | 频率 |
69.5~75.5 | 9 | 0.18 |
75.5~81.5 | m | 0.16 |
81.5~87.5 | 14 | 0.28 |
87.5~93.5 | 16 | n |
93.5~99.5 | 3 | 0.06 |
(1)表中n= ,并在图中补全频数直方图.
(2)甲同学的比赛成绩是50位参赛选手成绩的中位数,据此推测他的成绩落在 分数段内;
(3)选拔赛时,成绩在93.5~99.5的三位选手中,男生2人,女生1人,学校从中随机确定2名选手参加全市决赛,请用列表法或树状图法求恰好是一名男生和一名女生的概率.