Question

【题目】如图，抛物线y=ax2+bx﹣经过点A（1，0）和点B（5，0），与y轴交于点C．

（1）求此抛物线的解析式;
（2）以点A为圆心，作与直线BC相切的⊙A，求⊙A的半径
（3）在直线BC上方的抛物线上任取一点P，连接PB，PC，请问：△PBC的面积是否存在最大值？若存在，求出这个最大值的此时点P的坐标；若不存在，请说明理由．

Answer 1

【答案】
（1）

解：

∵抛物线y=ax2+bx﹣经过点A（1，0）和点B（5，0），

∴把A、B两点坐标代入可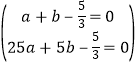得，解得，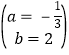

∴抛物线解析式为y=x2+2x﹣

（2）

解：过A作AD⊥BC于点D，如图1，

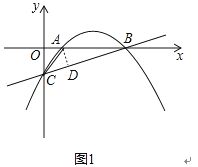
∵⊙A与BC相切，

∴AD为⊙A的半径，

由（1）可知C（0，），且A（1，0），B（5，0），

∴OB=5，AB=OB﹣OA=4，OC=，

在Rt△OBC中，由勾股定理可得BC===，

∵∠ADB=∠BOC=90°，∠ABD=∠CBO，

∴△ABD∽△CBO，

∴，即，解得AD=，

即⊙A的半径为

（3）

解：

∵C（0，），

∴可设直线BC解析式为y=kx﹣，

把B点坐标代入可求得k=，

∴直线BC的解析式为y=x﹣，

过P作PQ∥y轴，交直线BC于点Q，交x轴于点E，如图2，

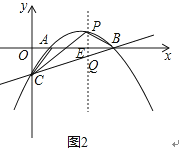
设P（x，x2+2x﹣），则Q（x，x﹣），

∴PQ=（x2+2x﹣）﹣（x﹣）=﹣x2+x=﹣（x﹣）2+，

∴S△PBC=S△PCQ+S△PBQ=PQOE+PQBE=PQ（OE+BE）=PQOB=PQ=﹣（x﹣）2+，

∴当x=时，S△PBC有最大值，此时P点坐标为（，），

∴当P点坐标为（，）时，△PBC的面积有最大值．

【解析】（1）把A、B两点分别代入抛物线解析可求得a和b，可求得抛物线解析式；
（2）过A作AD⊥BC于点D，则AD为⊙A的半径，由条件可证明△ABD∽△CBO，利用相似三角形的性质可求得AD的长，可求得半径；
（3）由待定系数法可求得直线BC解析式，过P作PQ∥y轴，交直线BC于点Q，交x轴于点E，可设出P、Q的坐标，可表示出△PQC和△PQB的面积，可表示出△PBC的面积，再利用二次函数的性质可求得其最大值，容易求得P点坐标．
【考点精析】本题主要考查了二次函数的图象和二次函数的性质的相关知识点，需要掌握二次函数图像关键点：1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点；增减性：当a>0时，对称轴左边，y随x增大而减小；对称轴右边，y随x增大而增大；当a<0时，对称轴左边，y随x增大而增大；对称轴右边，y随x增大而减小才能正确解答此题．