Question

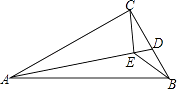
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=6，BC=8，点D为边CB上的一个动点（点D不与点B重合），过D作DO⊥AB，垂足为O，点B′在边AB上，且与点B关于直线DO对称，连接DB′，AD．

（1）求证：△DOB∽△ACB；
（2）若AD平分∠CAB，求线段BD的长；
（3）当△AB′D为等腰三角形时，求线段BD的长．

Answer 1

【答案】
（1）

证明：∵DO⊥AB，

∴∠DOB=∠DOA=90°，

∴∠DOB=∠ACB=90°，

又∵∠B=∠B，

∴△DOB∽△ACB；

（2）

解：∵∠ACB=90°，

∴AB===10，

∵AD平分∠CAB，DC⊥AC，DO⊥AB，

∴DC=DO，

在Rt△ACD和Rt△AOD中，

，

∴Rt△ACD≌Rt△AOD（HL），

∴AC=AO=6，

设BD=x，则DC=DO=8﹣x，OB=AB﹣AO=4，

在Rt△BOD中，根据勾股定理得：DO2+OB2=BD2，

即（8﹣x）2+42=x2，

解得：x=5，

∴BD的长为5；

（3）

解：∵点B′与点B关于直线DO对称，

∴∠B=∠OB′D，BO=B′O，BD=B′D，

∵∠B为锐角，

∴∠OB′D也为锐角，

∴∠AB′D为钝角，

∴当△AB′D为等腰三角形时，AB′=DB′，

∵△DOB∽△ACB，

∴==，

设BD=5x，

则AB′=DB′=5x，BO=B′O=4x，

∵AB′+B′O+BO=AB，

∴5x+4x+4x=10，

解得：x=，

∴BD=．

【解析】（1）由∠DOB=∠ACB=90°，∠B=∠B，容易证明△DOB∽△ACB；
（2）先由勾股定理求出AB，由角平分线的性质得出DC=DO，再由HL证明Rt△ACD≌Rt△AOD，得出AC=AO，设BD=x，则DC=DO=8﹣x，由勾股定理得出方程，解方程即可；
（3）根据题意得出当△AB′D为等腰三角形时，AB′=DB′，由△DOB∽△ACB，得出，设BD=5x，则AB′=DB′=5x，BO=B′O=4x，由AB′+B′O+BO=AB，得出方程，解方程求出x，即可得出BD．
【考点精析】认真审题，首先需要了解相似图形(形状相同，大小不一定相同（放大或缩小）;判定:①平行；②两角相等；③两边对应成比例，夹角相等；④三边对应成比例)．