题目内容
【题目】下表是某中学足球冠军杯第一阶段
组赛不完整的积分表．组共
个队，每个队分别与其它
个队进行主客场比赛各一场，即每个队都要进行
场比赛．每队每场比赛积分都是自然数．（总积分
胜场积分
平场积分负场积分）
球队 | 比赛场次 | 胜场次数 | 平场次数 | 负场次数 | 总积分 |
战神队 |
|
|
|
|
|
旋风队 |
|
|
| ||
龙虎队 |
|
|
|
|
|
梦之队 |
|
|
本次足球小组赛中，平一场积___________分，梦之队总积分是___________分．
【答案】1 0
【解析】
根据旋风队平两场积2分即可得出平一场的分数，然后根据战神队和龙虎队的成绩得出负一场的分数即可求梦之队的总分．
∵旋风队平两场积2分
∴平一场积1分
对比战神队和龙虎队的成绩发现，胜一场比平一场多积2分，所以胜一场积3分，
设负一场得x分，则有
解得
∴负一场积0分
因为梦之队负两场，所以积0分
故答案为：1；0．
名师指导期末冲刺卷系列答案
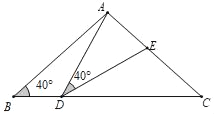
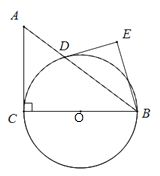
开心蛙口算题卡系列答案
【题目】如图，在Rt△ABC中，∠ACB=90°，AC=3，BC=4，以边BC为直径作⊙O，交AB于D，DE是⊙O的切线，过点B作DE的垂线，垂足为E．
(1)求证∠ABC＝∠ABE；
(2)求DE的长．
【题目】市园林处为了对一段公路进行绿化，计划购买
，
两种风景树共900棵．，两种树的相关信息如下表：
品种 项目 | 单价（元 | 成活率 |
| 80 |
|
| 100 |
|
若购买种树
棵，购树所需的总费用为
元．
（1）求与之间的函数关系式；
（2）若购树的总费用不超过82 000元，则购种树不少于多少棵？
（3）若希望这批树的成活率不低于
，且使购树的总费用最低，应选购，两种树各多少棵？此时最低费用为多少？
【题目】如图1，将边长为1的正方形ABCD压扁为边长为1的菱形ABCD．在菱形ABCD中，∠A的大小为α，面积记为S．
（1）请补全下表：
30° | 45° | 60° | 90° | 120° | 135° | 150° | |
S |
| 1 |
|
（2）填空：
由（1）可以发现正方形在压扁的过程中，菱形的面积随着∠A大小的变化而变化，不妨把菱形的面积S记为S(α)．例如：当α＝30°时，
；当α＝135°时，
．由上表可以得到
( ______°)；
( ______°)，…，由此可以归纳出
．
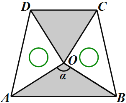
（3） 两块相同的等腰直角三角板按如图的方式放置，AD＝
，∠AOB＝α，试探究图中两个带阴影的三角形面积是否相等，并说明理由（注：可以利用（2）中的结论）．
