��Ŀ����
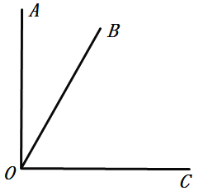
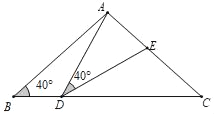
����Ŀ����ͼ���ڡ�ABC�У�AB��AC��2����B����C��40�㣬��D���߶�BC���˶�����D�����B��C�غϣ�������AD������ADE��40�㣬DE���߶�AC�ڵ�E��
��1������BDA��110��ʱ����EDC���� ���㣬��DEC���� ���㣻��D��B��C���˶������У���BDA���� �������С������
��2����DC���ڶ���ʱ����ABD�ա�DCE����˵�����ɣ�
��3���ڵ�D���˶������У���ADE����״�����ǵ����������������ԣ���ֱ��д����BDA�Ķ������������ԣ���˵�����ɣ�
���𰸡���1��30��110��С����2����DC��2ʱ����ABD�ա�DCE�����������������3������BDA��80���110��ʱ����ADE����״�����ǵ���������.
��������
��1�������ڲ��ǵ����ʺ������ε���ǵ��ڲ����ڵ����ڽǺ���һ���ʽ��⣬
��2����DC=2ʱ�����á�ADC����B+��BAD����ADC����ADE+��CDE���
��BAD����CDE��������AB��CD��2����B����C��40���ó���ABD�ա�DCE.
��3��������ADE�ǵ��������Σ�������������ֱ�������÷�������Ľ�.
�⣺��1���ߡ�ADB+��ADE+��EDC��180�����ҡ�ADE��40������BDA��110����
���EDC��30����
�ߡ�AED����EDC+��ACB��30��+40����70��
���EDC��180������AED��110����
�ʴ�Ϊ��30��110��
�ߡ�BDA+��B+��BAD��180����
���BDA��140������BAD
�ߵ�D��B��C���˶������У���BAD���
���BDA����
�ʴ�Ϊ��С
��2����DC��2ʱ����ABD�ա�DCE��
�������£��ߡ�ADC����B+��BAD����ADC����ADE+��CDE����B����ADE��40����
���BAD����CDE����AB��CD��2����B����C��40����
���ABD�ա�DCE��ASA��
��3����AD��DEʱ��
��AD��DE����ADE��40��
���DEA����DAE��70��
�ߡ�DEA����C+��EDC
���EDC��30��
���BDA��180������ADE����EDC��180����40����30����110��
��AE��DEʱ��
��AE��DE����ADE��40��
���ADE����DAE��40����
���AED��100��
�ߡ�DEA����C+��EDC
���EDC��60��
���BDA��180������ADE����EDC��180����40����60����80��
��������������BDA��80����110��ʱ����ADE����״�����ǵ���������.

 ��У����ϵ�д�
��У����ϵ�д�����Ŀ���±���ij��ѧ����ھ�����һ��![]() �����������Ļ��ֱ���
�����������Ļ��ֱ���![]() �鹲
�鹲![]() ���ӣ�ÿ���ӷֱ�������
���ӣ�ÿ���ӷֱ�������![]() ���ӽ������ͳ�������һ������ÿ���Ӷ�Ҫ����
���ӽ������ͳ�������һ������ÿ���Ӷ�Ҫ����![]() ��������ÿ��ÿ���������ֶ�����Ȼ�������ܻ���
��������ÿ��ÿ���������ֶ�����Ȼ�������ܻ���![]() ʤ������
ʤ������![]() ƽ������
ƽ������![]() �������֣�
�������֣�
��� | �������� | ʤ������ | ƽ������ | �������� | �ܻ��� |
ս��� |
|
|
|
|
|
����� |
|
|
| ||
������ |
|
|
|
|
|
��֮�� |
|
|
��������С�����У�ƽһ����___________�֣���֮���ܻ�����___________�֣�