题目内容
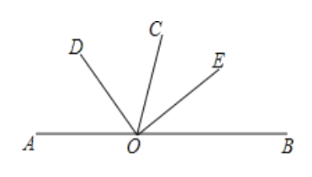
【题目】根据给出的数轴及已知条件,解答下面的问题:
![]()
(1)已知点A,B,C表示的数分别为1,![]() ,-3.观察数轴,与点A的距离为3的点表示的数是 ,A,B两点之间的距离为 。
,-3.观察数轴,与点A的距离为3的点表示的数是 ,A,B两点之间的距离为 。
(2)数轴上,点B关于点A的对称点表示的数是 ;
(3)若将数轴折叠,使得A点与C点重合,则与B点重合的点表示的数是 ;若此数轴上M,N两点之间的距离为2019(M在N的左侧),且当A点与C点重合时,M点与N点也恰好重合,则点M表示的数是 ,点N表示的数是 。
(4)若数轴上P,Q两点间的距离为a(P在Q的左侧),表示数b的点到P,Q的两点的距离相等,将数轴折叠,当P点与Q点重合时,点P表示的数是 ,点Q表示的数是 (用含a,b的式子表示这两个数)。
【答案】(1)4或-2;![]() ;(2)4.5;(3)
;(2)4.5;(3)![]() ,-1010.5,1008.5(3)b-
,-1010.5,1008.5(3)b-![]() ,b+
,b+![]() .
.
【解析】
(1)分点在A的左边和右边两种情况解答;利用两点之间的距离计算方法直接计算得出答案即可;
(2)点B关于点A的对称点在点A右侧,且与B到A的距离相等即可求得;
(3)A点与C点重合,得出对称点位-1,然后根据两点之间的距离列式计算即可得解;
(4)根据(3)的计算方法,然后分别列式计算即可得解.
(1)点A的距离为3的点表示的数是1+3=4或1-3=-2;
A,B两点之间的距离为1-(![]() )=
)=![]() ;
;
故答案为:4或-2;![]()
(2)设点B关于点A的对称点表示的数是x,
则x-1=1-(![]() ),
),
解得x=4.5,
故答案为:4.5;
(3)B点重合的点表示的数是:-1+[-1-(![]() )]=
)]=![]() ;
;
M=-1-![]() =-1010.5,n=-1+
=-1010.5,n=-1+![]() =1008.5;
=1008.5;
故答案为:-1010.5,1008.5
(4)P=b-![]() ,Q=b+
,Q=b+![]() .
.
故答案为:b-![]() ,b+
,b+![]() .
.

 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案【题目】下表是某中学足球冠军杯第一阶段![]() 组赛不完整的积分表.
组赛不完整的积分表.![]() 组共
组共![]() 个队,每个队分别与其它
个队,每个队分别与其它![]() 个队进行主客场比赛各一场,即每个队都要进行
个队进行主客场比赛各一场,即每个队都要进行![]() 场比赛.每队每场比赛积分都是自然数.(总积分
场比赛.每队每场比赛积分都是自然数.(总积分![]() 胜场积分
胜场积分![]() 平场积分
平场积分![]() 负场积分)
负场积分)
球队 | 比赛场次 | 胜场次数 | 平场次数 | 负场次数 | 总积分 |
战神队 |
|
|
|
|
|
旋风队 |
|
|
| ||
龙虎队 |
|
|
|
|
|
梦之队 |
|
|
本次足球小组赛中,平一场积___________分,梦之队总积分是___________分.