题目内容
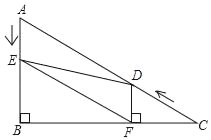
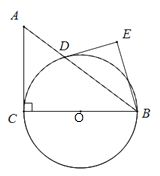
【题目】如图,在Rt△ABC中,∠ACB=90°,AC=3,BC=4,以边BC为直径作⊙O,交AB于D,DE是⊙O的切线,过点B作DE的垂线,垂足为E.
(1)求证∠ABC=∠ABE;
(2)求DE的长.
【答案】(1)见解析;(2)![]()
【解析】分析:(1)、连接OD,根据切线的性质以及BE⊥DE得出OD∥BE,结合OD=OB得出∠ABC=∠ABE;(2)、连接CD,根据题意得出△BDC和△BCA相似,从而得出BD的长度,然后根据△DEB和△ACB相似得出DE的长度.
详解:(1)证明:连接OD,∵DE是⊙O的切线;∴OD⊥DE, ∵BE⊥DE,∴OD∥BE,
∴∠EBD=∠ODB,∵OD=OB, ∴∠ODB=∠ABC, ∴∠ABC=∠ABE;
(2)连接CD,在Rt△ABC中,AC=3,BC=4,∴AB=5, ∵⊙O的半径,∴∠CDB=90°,
∵∠ACB=90°, ∴∠ACB=∠CDB, ∵∠B=∠B, ∴△BDC∽△BCA,
∴![]() ,即
,即![]() , ∴BD=
, ∴BD=![]() , ∵∠ACB=∠DEB=90°,∠ABC=∠ABE,
, ∵∠ACB=∠DEB=90°,∠ABC=∠ABE,
∴△DEB∽△ACB, ∴![]() ,即
,即![]() , ∴DE=
, ∴DE=![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
【题目】下表是某中学足球冠军杯第一阶段![]() 组赛不完整的积分表.
组赛不完整的积分表.![]() 组共
组共![]() 个队,每个队分别与其它
个队,每个队分别与其它![]() 个队进行主客场比赛各一场,即每个队都要进行
个队进行主客场比赛各一场,即每个队都要进行![]() 场比赛.每队每场比赛积分都是自然数.(总积分
场比赛.每队每场比赛积分都是自然数.(总积分![]() 胜场积分
胜场积分![]() 平场积分
平场积分![]() 负场积分)
负场积分)
球队 | 比赛场次 | 胜场次数 | 平场次数 | 负场次数 | 总积分 |
战神队 |
|
|
|
|
|
旋风队 |
|
|
| ||
龙虎队 |
|
|
|
|
|
梦之队 |
|
|
本次足球小组赛中,平一场积___________分,梦之队总积分是___________分.