��Ŀ����
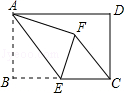
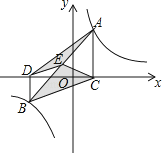
����Ŀ����ͼ1�����߳�Ϊ1��������ABCDѹ��Ϊ�߳�Ϊ1������ABCD��������ABCD�У���A�Ĵ�СΪ���������ΪS��

��1���벹ȫ�±���
30�� | 45�� | 60�� | 90�� | 120�� | 135�� | 150�� | |
S |
| 1 |
|
��2����գ�
�ɣ�1�����Է�����������ѹ��Ĺ����У����ε�������š�A��С�ı仯���仯�����������ε����S��ΪS(��)�����磺������30��ʱ��![]() ��������135��ʱ��
��������135��ʱ��![]() �����ϱ����Եõ�
�����ϱ����Եõ�![]() ( ______��)��
( ______��)��![]() ( ______��)�������ɴ˿��Թ��ɳ�
( ______��)�������ɴ˿��Թ��ɳ�![]() ��
��
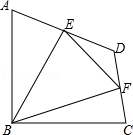
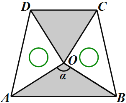
��3�� ������ͬ�ĵ���ֱ�����ǰ尴��ͼ�ķ�ʽ���ã�AD��![]() ����AOB��������̽��ͼ����������Ӱ������������Ƿ���ȣ���˵�����ɣ�ע���������ã�2���еĽ��ۣ���
����AOB��������̽��ͼ����������Ӱ������������Ƿ���ȣ���˵�����ɣ�ע���������ã�2���еĽ��ۣ���
���𰸡���1��![]() ��
��![]() ��
��![]() ��
��![]() ����2��120��30��������3����������Ӱ�������������ȣ�֤��������.
����2��120��30��������3����������Ӱ�������������ȣ�֤��������.
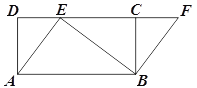
����������1����D��DE��AB�ڵ�E������=45��ʱ�������DE���Ӷ���������ε����S��ͬ��������=60��ʱS��ֵ������=120��ʱ����D��DF��AB��BA���ӳ����ڵ�F��������DF�������S��ֵ��ͬ������=135��ʱS��ֵ��
��2�����ݱ������������S��ֵ���ɵó��𰸣�
��3������ABO��AB���۵õ�����AEBO������CDO��CD���۵õ�����OCFD�����ã�2���еĽ��ۣ��������AOB����COD��������Ӷ�����ý��ۣ�
��1������=45��ʱ����ͼ1����D��DE��AB�ڵ�E��
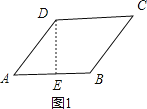
��DE=![]() AD=
AD=![]() ��
��
��S=ABDE=![]() ��
��
ͬ������=60��ʱS=![]() ��
��
����=120��ʱ����ͼ2����D��DF��AB����BA���ӳ����ڵ�F��
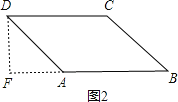
���DAE=60�㣬
��DF=![]() AD=
AD=![]() ��
��
��S=ABDF=![]() ��
��
ͬ������=150��ʱ�������S=![]() ��
��
�ʱ���������д��![]() ��
��![]() ��
��![]() ��
��![]() ��
��
��2���ɣ�1����֪S��60�㣩=S��120�㣩��
S��150�㣩=S��30�㣩��
��S��180��-����=S������
�ʴ�Ϊ��120��30������
��3����������Ӱ�������������ȣ�
֤������ͼ3����ABO��AB���۵õ�����AMBO������CDO��CD���۵õ�����OCND��
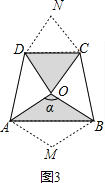
�ߡ�AOD=��COB=90�㣬
���COD+��AOB=180�㣬
��S��AOB=![]() S����AMBO=
S����AMBO=![]() S������
S������
S��CDO=![]() S����OCND=
S����OCND=![]() S��180��-����
S��180��-����
�ɣ�2���н���S������=S��180��-����
��S��AOB=S��CDO��

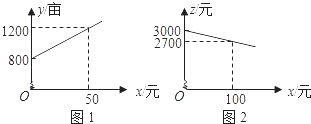
����Ŀ������Ժ�칫��2015��3��16�շ����ˡ��й�����ĸ�����巽�����������й�������ʷ�ϵ��ش�ĸΪ�˽�һ���ռ�����֪ʶ�����������Ļ������о����ˡ������У��֪ʶ�������Ϊ�˽�����֪ʶ���ռ�����������ȡ�˲��ֻ���������������õ����в�������ͳ��ͼ����
�ȴ� | Ƶ�� | Ƶ�� |
һ�Ƚ� | 10 | 0.05 |
���Ƚ� | 20 | 0.10 |
���Ƚ� | 30 | b |
��ʤ�� | a | 0.30 |
������ | 80 | 0.40 |
�����������Ϣ������������⣺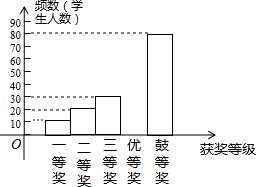
��1��a= �� b= �� �Ҳ�ȫƵ���ֲ�ֱ��ͼ��
��2����������ͳ��ͼ�������ֲ�������ʻ����ʤ����Ӧ������Բ�ĽǵĶ����Ƕ��٣�
��3������ξ����У��ס��ҡ���������λͬѧ�����һ�Ƚ�����������λͬѧ�����ѡȡ��λͬѧ�������вμ���һ��������������״ͼ���б��ķ���������ǡ��ѡ�мס��Ҷ��˵ĸ��ʣ�