题目内容
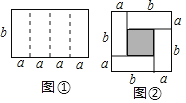
【题目】如图①是一个长为4a、宽为b的长方形,沿图中虚线用剪刀将其平均分成四块小长方形,然后用四块小长方形拼成一个“回形”正方形(如图②)
自主探索:
(1)仔细观察图形,完成下列问题
①图②中的阴影部分的面积为_____;
②观察图②,请你写出(a+b)2、(a-b)2、ab之间的等量关系是_____;
知识运用:
(2)若x-y=5,xy=![]() ,根据(1)中的结论,求(x+y)2的值;
,根据(1)中的结论,求(x+y)2的值;
知识延伸
(3)根据你探索发现的结论,完成下列问题:
设A=![]() ,B=x+2y-3
,B=x+2y-3
计算(A-B)2-(A+B)2的结果.
【答案】(1)①阴影部分的面积为(b-a)2,②(a+b)2=(b-a)2+4ab;(2)36;(3)4y2-x2+6x-9.
【解析】
(1)①阴影部分面积直接利用边长乘边长即可 ②利用正方形面积等于空白部分面积加上阴影部分面积即可 (2)(x+y)2=(x-y)2+4xy代入求值即可 (3)(A-B)2-(A+B)2= A2-2AB+B2-A2-2AB-B2=-4AB,代入A、B计算即可
(1)①图②中的阴影部分的面积为(b-a)2,
②由图2知,(a+b)2、(a-b)2、ab之间的等量关系是(a+b)2=(b-a)2+4ab,即(a+b)2=(a-b)2+4ab,
故答案为:(b-a)2、(a+b)2=(b-a)2+4ab;
(2)(x+y)2=(x-y)2+4xy
=52+4×![]()
=25+11
=36;
(3)当A=![]() ,B=x+2y-3时,
,B=x+2y-3时,
原式=A2-2AB+B2-A2-2AB-B2
=-4AB
=-4×![]() ×(x+2y-3)
×(x+2y-3)
=-(x-2y-3)(x+2y-3)
=-[(x-3)2-4y2]
=-(x2-6x+9-4y2)
=4y2-x2+6x-9.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目