题目内容
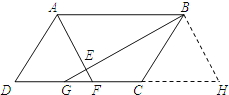
【题目】如图,在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点F、G,
AF与BG交于点E.

(1)求证:AF⊥BG,DF=CG;
(2)若AB=10,AD=6,AF=8,求FG和BG的长度.
【答案】(1)见解析(2)FG的长度为2,BG的长度为4![]() .
.
【解析】
试题分析:(1)由在平行四边形ABCD中,∠BAD、∠ABC的平分线AF、BG分别与线段CD交于点F、G,易求得2∠BAF+2∠ABG=180°,即可得∠AEB=90°,证得AF⊥BG,易证得△ADF与△BCG是等腰三角形,即可得AD=DF,BC=CG,又由AD=BC,即可证得DF=CG;
(2)由(1)易求得DF=CG=8,CD=AB=10,即可求得FG的长;过点B作BH∥AF交DC的延长线于点H,易证得四边形ABHF为平行四边形,即可得△HBG是直角三角形,然后利用勾股定理,即可求得BG的长.
(1)证明:∵AF平分∠BAD,
∴∠DAF=∠BAF=![]() ∠BAD.
∠BAD.
∵BG平分∠ABC,
∴∠ABG=∠CBG=![]() ∠ABC.
∠ABC.
∵四边形ABCD平行四边形,
∴AD∥BC,AB∥CD,AD=BC,
∴∠BAD+∠ABC=180°,
即2∠BAF+2∠ABG=180°,
∴∠BAF+∠ABG=90°.
∴∠AEB=180°﹣(∠BAF+∠ABG)=180°﹣90°=90°.
∴AF⊥BG;
∵AB∥CD,
∴∠BAF=∠AFD,
∴∠AFD=∠DAF,
∴DF=AD,
∵AB∥CD,
∴∠ABG=∠CGB,
∴∠CBG=∠CGB,
∴CG=BC,
∵AD=BC.
∴DF=CG;
(2)解:∵DF=AD=6,
∴CG=DF=6.
∴CG+DF=12,
∵四边形ABCD平行四边形,
∴CD=AB=10.
∴10+FG=12,
∴FG=2,
过点B作BH∥AF交DC的延长线于点H.
∴∠GBH=∠AEB=90°.
∵AF∥BH,AB∥FH,
∴四边形ABHF为平行四边形.
∴BH=AF=8,FH=AB=10.
∴GH=FG+FH=2+10=12,
∴在Rt△BHG中:BG=![]() =
=![]() .
.
∴FG的长度为2,BG的长度为4![]() .
.


 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案