题目内容
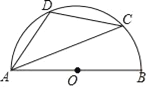
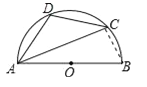
【题目】如图，AB是半圆的直径，C、D是半圆上的两点，且∠BAC=20°，
．请连结线段CB，求四边形ABCD各内角的度数．
【答案】55°，70°，125°，110°
【解析】试题分析：连结BC，根据圆周角定理得∠ACB=90°，则利用互余可计算出∠B=70°，再根据圆内接四边形的性质计算出∠D=180°﹣∠B=110°，接着根据圆周角定理和三角形内角和定理，由弧AD=弧CD得到∠DAC=∠DCA=35°，然后计算∠DAB=∠DAC+∠BAC=55°，∠DCB=∠DCA+∠ACB=125°．
试题解析：解：连结BC，如图，∵AB是半圆的直径，∴∠ACB=90°，∵∠BAC=20°，∴∠B=70°，∵四边形ABCD是圆O的内接四边形，∴∠D=180°﹣∠B=110°，∵弧AD=弧CD，∴∠DAC=∠DCA=
（180°-110°）=35°，∴∠DAB=∠DAC+∠BAC=55°，∠DCB=∠DCA+∠ACB=125°，即四边形ABCD各内角的度数分别为55°，70°，125°，110°．
【题目】某市举行知识大赛，A校、B校各派出5名选手组成代表队参加决赛，两校派出选手的决赛成绩如图所示．
根据图示填写下表：
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
结合两校成绩的平均数和中位数，分析哪个学校的决赛成绩较好；
计算两校决赛成绩的方差，并判断哪个学校代表队选手成绩较为稳定．
【题目】盒中有若干枚黑棋和白棋，这些棋除颜色外无其他差别，现让学生进行摸棋试验：每次摸出一枚棋，记录颜色后放回摇匀，重复进行这样的试验得到以下数据：
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | b | 201 | 250 |
摸到黑棋的频率 | 0.240 | a | 0.253 | 0.248 | 0.251 | 0.250 |
（1）填空：a= ，b= ；
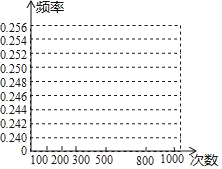
（2）在图中，画出摸到黑棋的折线统计图；
（3）随机摸一次，估计摸到黑棋的概率．（精确到0.01）
