题目内容
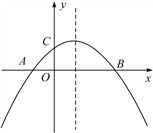
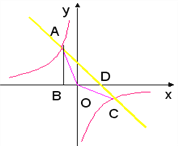
【题目】点A是双曲线![]() 与直线
与直线![]() 在第二象限的交点,AB垂直
在第二象限的交点,AB垂直![]() 轴于点B,且S△ABO=
轴于点B,且S△ABO=![]() .
.
(1)求两个函数的表达式;
(2)求直线与双曲线的交点坐标和△AOC的面积.
【答案】(1)![]() ,
, ![]() ;(2)4.
;(2)4.
【解析】试题分析:
(1)由S△ABO=![]() 可得反比例函数
可得反比例函数![]() 中,
中, ![]() 结合点A在第二象限,可得
结合点A在第二象限,可得![]() ,由此即可求得反比例函数和一次函数的解析式;
,由此即可求得反比例函数和一次函数的解析式;
(2)由(1)中所得的两个函数的解析式组成方程组,解方程组即可得到点A、C的坐标;由一次函数的解析式可求得点D的坐标,这样即可由S△AOC=S△AOD+S△COD求出△AOC的面积了.
试题解析:
(1)设点![]() 的坐标为(
的坐标为(![]() )
)
∵![]() ∣
∣![]() ∣=
∣=![]()
∴ ∣![]() ∣=3 ∴∣k∣=3
∣=3 ∴∣k∣=3
∵点![]() 在第二象限 ∴k=
在第二象限 ∴k= ![]()
∴反比例函数的解析式为![]() ,一次函数的解析式为
,一次函数的解析式为![]() ;
;
(2)由: 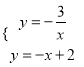 ,解得
,解得 ![]()
![]()
∴点![]() 的坐标为(
的坐标为(![]() )
) ![]() 点的坐标(
点的坐标(![]() )
)
设直线![]() 与
与![]() 轴交于点
轴交于点![]() ,则由
,则由![]() 可解得
可解得![]() ,
,
∴![]() 点坐标为 (
点坐标为 (![]() )
)
∴![]()
![]() .
.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
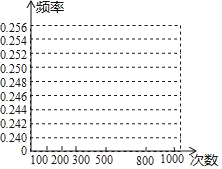
【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀,重复进行这样的试验得到以下数据:
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | b | 201 | 250 |
摸到黑棋的频率 | 0.240 | a | 0.253 | 0.248 | 0.251 | 0.250 |
(1)填空:a= ,b= ;
(2)在图中,画出摸到黑棋的折线统计图;
(3)随机摸一次,估计摸到黑棋的概率.(精确到0.01)