题目内容
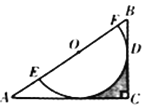
【题目】如图,△ABC中,点O是AC边上的一个动点,过点O作直线MN∥BC,设MN交∠BCA的平分线于点E,交∠BCA的外角平分线于点F.
(1)判断OE与OF的大小关系?并说明理由?
(2)当点O运动何处时,四边形AECF是矩形?并说出你的理由.

【答案】(1)证OE=OC,OF=OC,推出OE=OF,
(2)当点O运动到AC的中点时,四边形AECF是矩形
【解析】试题分析:
(1)先判断∠ECF=90°,再利用角平分线,平行线,等腰三角形的关系得到OE=OC,OF=OC;
(2)结合(1)中的结论,利用对角线相等的平行四边形是矩形说明.
试题解析:
(1)OE=OF,理由如下:
∵CE,CF分别是∠ACB和∠ACB外角的平分线,
∴∠ACE=∠BCE=![]() ∠ACB,∠ACF=∠GCF=
∠ACB,∠ACF=∠GCF=![]() ∠ACG.
∠ACG.
∴∠ECF=∠ACE+∠ACF=![]() ∠ACB+
∠ACB+![]() ∠ACG=
∠ACG=![]() (ACB+∠ACG)=
(ACB+∠ACG)=![]() ∠BCG=90°.
∠BCG=90°.
∵MN∥BC,∴∠FEC=∠BCE,∴∠FEC=∠ACE,∴OE=OC.
同理OF=OC,所以OE=OF.
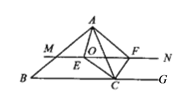
(2)由(1)得,OC=OE=OF,所以当OA=OC时,对角线AC与EF互相平分且相等,而对角线相等的平行四边形是矩形,则当点O运动到AC的中点时,四边形AECF是矩形.

 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
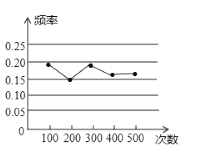
名校名卷单元同步训练测试题系列答案【题目】某市举行知识大赛,A校、B校各派出5名选手组成代表队参加决赛,两校派出选手的决赛成绩如图所示.
![]() 根据图示填写下表:
根据图示填写下表:
平均数 | 中位数 | 众数 | |
A校 | ______ | 85 | ______ |
B校 | 85 | ______ | 100 |
![]() 结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
结合两校成绩的平均数和中位数,分析哪个学校的决赛成绩较好;
![]() 计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.
计算两校决赛成绩的方差,并判断哪个学校代表队选手成绩较为稳定.

【题目】盒中有若干枚黑棋和白棋,这些棋除颜色外无其他差别,现让学生进行摸棋试验:每次摸出一枚棋,记录颜色后放回摇匀,重复进行这样的试验得到以下数据:
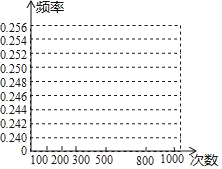
摸棋的次数n | 100 | 200 | 300 | 500 | 800 | 1000 |
摸到黑棋的次数m | 24 | 51 | 76 | b | 201 | 250 |
摸到黑棋的频率 | 0.240 | a | 0.253 | 0.248 | 0.251 | 0.250 |
(1)填空:a= ,b= ;
(2)在图中,画出摸到黑棋的折线统计图;
(3)随机摸一次,估计摸到黑棋的概率.(精确到0.01)