题目内容
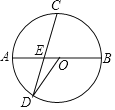
【题目】已知:如图,![]() 是⊙
是⊙![]() 上一点,半径
上一点,半径![]() 的延长线与过点
的延长线与过点![]() 的直线交于点
的直线交于点![]() ,
,![]() .
.
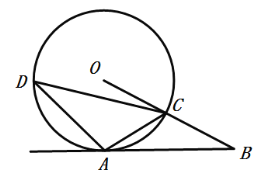
(1)求证:![]() 是⊙
是⊙![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,求弦
,求弦![]() 的长.
的长.
【答案】(1)见解析;(2)![]() .
.
【解析】
(1)利用题中的边的关系可求出△OAC是等边三角形,然后利用角边关系又可求出∠CAB=30°,从而求出∠OAB=90°,所以判断出直线AB与⊙O相切;
(2)作AE⊥CD于点E,由已知条件得出AC=2,再求出AE=CE,根据解直角三角形就可以得到DE,从而得出答案.
(1)证明:连接OA,则OA=OC.
∵OC=AC
∴△OAC是等边三角形
∴∠OAC=∠OCA=∠AOC=60
∵AC=BC
∴∠CAB=∠B
∵∠OCA是△ACB的外角
∴∠OCA=∠CAB+∠B
∴![]()
∴∠OAB=∠OAC+∠CAB=90
即:OA⊥AB
∴AB是⊙O的切线。
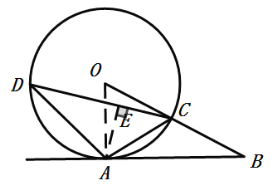
(2)解:过点A作AE⊥CD于点E
∵△OAC是等边三角形 ∴AC=OC=2
在Rt△AEC中,![]()
AE=AC·sin∠ACD=2×sin45=![]()
CE=AC·cos∠ACD=2×cos45=![]()
∵∠D=![]() ∠AOC=30
∠AOC=30
∴在Rt△AED中,
∴![]() .
.

练习册系列答案
 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案
相关题目