题目内容
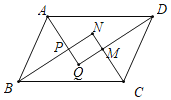
【题目】如图,在![]() 中,
中,![]() 分别是
分别是![]() 的中点,
的中点,![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() .
.
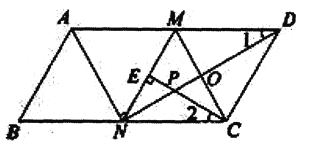
(1)求证:![]() ;
;
(2)过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的长.
的长.
【答案】(1)见解析;(2)AN的长为2![]() .
.
【解析】
(1)利用平行四边形的性质及中点的性质即可证得结论;
(2)先判定四边形CDMN是平行四边形,再判断其为菱形,利用菱形的性质,判断△MNC为等边三角形,从而求得∠1=∠2=∠MND=30°,在![]() 中,利用特殊角,求出EN,进而求出线段AN的长.
中,利用特殊角,求出EN,进而求出线段AN的长.
(1)在平行四边形ABCD中,∠B=∠ADC,AB=CD,
∵M,N分别是AD,BC的中点,
∴BN=![]() BC=
BC=![]() AD=DM,
AD=DM,
∴△ABN ≌△CDM;
(2)∵在平行四边形ABCD中,M,N分别是AD,BC的中点,
∴![]() ,
,![]() ,
,
∴四边形CDMN为平行四边形,
∵在![]() 中,M为AD中点,
中,M为AD中点,
∴ MN=MD,
∴平行四边形CDMN为菱形;
∴∠MND=∠DNC=∠1=∠2,
∵CE⊥MN,∠MND+∠DNC+∠2=90°,
∴∠MND=∠DNC=∠2=30°,
在![]() 中,∵PE=1,∠ENP=30°,
中,∵PE=1,∠ENP=30°,
∴EN=![]() ,
,
在![]() 中,∵EN=
中,∵EN=![]() ,∠2=30°,
,∠2=30°,
NC=2 EN =2![]() ,
,
∵∠MNC=∠MND+∠DNC=60°,
∴△MNC为等边三角形,又由(1)可得,MC=AN,
∴AN=MC=NC=2![]() ,
,
∴AN的长为2![]() .
.

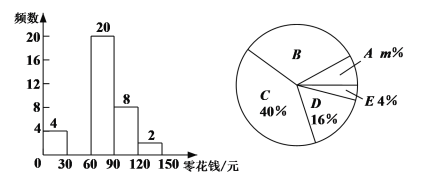
【题目】某学校为了解学生的课外阅读情况,随机抽取了50名学生,并统计他们平均每天的课外阅读时间t(单位:min),然后利用所得数据绘制成如下不完整的统计表.
课外阅读时间t | 频数 | 百分比 |
10≤t<30 | 4 | 8% |
30≤t<50 | 8 | 16% |
50≤t<70 | a | 40% |
70≤t<90 | 16 | b |
90≤t<110 | 2 | 4% |
合计 | 50 | 100% |
请根据图表中提供的信息回答下列问题:
(1)a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若全校有900名学生,估计该校有多少学生平均每天的课外阅读时间不少于50min?