题目内容
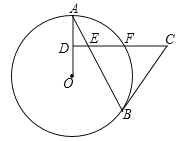
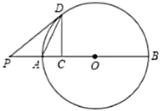
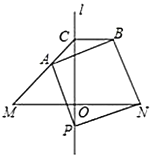
【题目】如图,直线![]() 是线段
是线段![]() 的垂直平分线,交线段
的垂直平分线,交线段![]() 于点
于点![]() ,在
,在![]() 下方的直线
下方的直线![]() 上取一点
上取一点![]() ,连接
,连接![]() ,以线段
,以线段![]() 为边,在
为边,在![]() 上方作正方形
上方作正方形![]() ,射线
,射线![]() 交直线
交直线![]() 于点
于点![]() ,连接
,连接![]() .
.
(1)设![]() ,求
,求![]() 的度数;
的度数;
(2)写出线段![]() 、
、![]() 之间的等量关系,并证明.
之间的等量关系,并证明.
【答案】(1)45° ;(2)![]() ,证明见解析.
,证明见解析.
【解析】
(1)由线段的垂直平分线的性质可得PM=PN,且PO⊥MN,由等腰三角形的性质可得∠PMN=∠PNM=α,由正方形的性质可得AP=PN,∠APN=90°,可得∠APO=α,由三角形的外角性质可求∠AMN的度数;
(2)由等腰直角三角形的性质和正方形的性质可得MN=![]() CN,AN=
CN,AN=![]() BN,∠MNC=∠ANB=45°,可证△CBN∽△MAN,可得AM=
BN,∠MNC=∠ANB=45°,可证△CBN∽△MAN,可得AM=![]() BC.
BC.
(1)如图,连接MP,
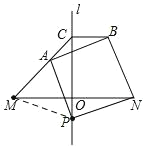
∵直线l是线段MN的垂直平分线,
∴PM=PN,且PO⊥MN
∴∠PMN=∠PNM=α
∴∠MPO=∠NPO=90°-α,
∵四边形ABNP是正方形
∴AP=PN,∠APN=90°
∴AP=MP,∠APO=90°-(90°-α)=α
∴∠APM=∠MPO-∠APO=(90°-α)-α=90°-2α,
∵AP=PM
∴∠PMA=∠PAM=![]() =45°+α,
=45°+α,
∴∠AMN=∠AMP-∠PMN=45°+α-α=45°
(2)AM=![]() BC
BC
理由如下:
如图,连接AN,CN,
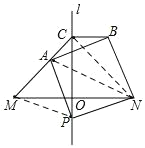
∵直线l是线段MN的垂直平分线,
∴CM=CN,
∴∠CMN=∠CNM=45°,
∴∠MCN=90°
∴MN=![]() CN,
CN,
∵四边形APNB是正方形
∴∠ANB=∠BAN=45°
∴AN=![]() BN,∠MNC=∠ANB=45°
BN,∠MNC=∠ANB=45°
∴∠ANM=∠BNC
又∵![]()
∴△CBN∽△MAN
∴![]()
∴AM=![]() BC
BC

 名校课堂系列答案
名校课堂系列答案【题目】丁老师为了解所任教的两个班的学生数学学习情况,对数学进行了一次测试,获得了两个班的成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
①A、B两班学生(两个班的人数相同)数学成绩不完整的频数分布直方图如下(数据分成5组:x<60,60≤x<70,70≤x<80,80≤x<90,90≤x≤100):
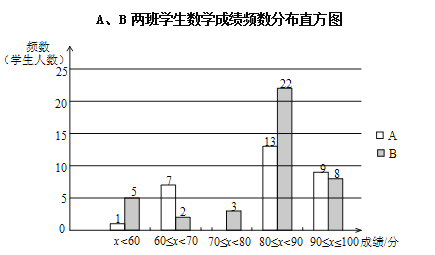
②A、B两班学生测试成绩在80≤x<90这一组的数据如下:
A班:80 80 82 83 85 85 86 87 87 87 88 89 89
B班:80 80 81 81 82 82 83 84 84 85 85 86 86 86 87 87 87 87 87 88 88 89
③A、B两班学生测试成绩的平均数、中位数、方差如下:
平均数 | 中位数 | 方差 | |
A班 | 80.6 | m | 96.9 |
B班 | 80.8 | n | 153.3 |
根据以上信息,回答下列问题:
(1)补全数学成绩频数分布直方图;
(2)写出表中m、n的值;
(3)请你对比分析A、B两班学生的数学学习情况(至少从两个不同的角度分析).