Question

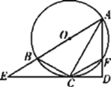
【题目】如图，AB是⊙O的直径，C是弧AB的中点，弦CD与AB相交于E．

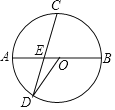
（1）若∠AOD＝45°，求证：CE＝ED；（2）若AE＝EO，求tan∠AOD的值．

Answer 1

【答案】（1）见解析；（2）tan∠AOD＝.

【解析】

（1）作DF⊥AB于F，连接OC，则△ODF是等腰直角三角形，得出OC=OD=DF，由垂径定理得出∠COE=90°，证明△DEF∽△CEO得出，即可得出结论；

（2）由题意得OE=OA=OC，同（1）得△DEF∽△CEO，得出，设⊙O的半径为2a（a＞0），则OD=2a，EO=a，设EF=x，则DF=2x，在Rt△ODF中，由勾股定理求出x=a，得出DF=a，OF=EF+EO=a，由三角函数定义即可得出结果．

（1）证明：作DF⊥AB于F，连接OC，如图所示：

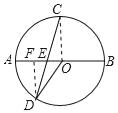
则∠DFE＝90°，

∵∠AOD＝45°，

∴△ODF是等腰直角三角形，

∴OC＝OD＝DF，

∵C是弧AB的中点，

∴OC⊥AB，

∴∠COE＝90°，

∵∠DEF＝∠CEO，

∴△DEF∽△CEO，

∴，

∴CE＝ED；

（2）如图所示：

∵AE＝EO，

∴OE=OA=OC，

同（1）得：，△DEF∽△CEO，

∴，

设⊙O的半径为2a（a＞0），则OD＝2a，EO＝a，

设EF＝x，则DF＝2x，

在Rt△ODF中，由勾股定理得：（2x）2+（x+a）2＝（2a）2，

解得：x＝a，或x＝﹣a（舍去），

∴DF＝a，OF＝EF+EO＝a，

∴．