题目内容
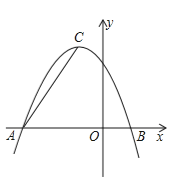
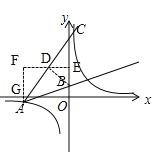
【题目】如图,已知点B(0,2),A(﹣6,﹣1)在反比例函数![]() 的图象上,作射线AB,再将射线AB绕点A逆时针旋转45°后,交反比例函数
的图象上,作射线AB,再将射线AB绕点A逆时针旋转45°后,交反比例函数![]() 图象于点C,则点C的坐标为_____.
图象于点C,则点C的坐标为_____.

【答案】(![]() ,18)
,18)
【解析】
过B作BD⊥AC于D,过D作DE⊥y轴于E,过A作AF⊥DE于F,则△ABD为等腰直角三角形,易得△AFD≌△DEB,依据全等三角形的性质,即可得出D(![]() ,
,![]() ),进而得出直线AD的解析式,解方程组即可得到C点坐标.
),进而得出直线AD的解析式,解方程组即可得到C点坐标.
解:如图所示,过B作BD⊥AC于D,过D作DE⊥y轴于E,过A作AF⊥DE于F,
∵AB绕点A逆时针旋转45°,BD⊥AC
∴∠DAB=∠DBA=45°
∴AD=BD,即△ABD为等腰直角三角形
又∵BD⊥AC,过D作DE⊥y轴于E,过A作AF⊥DE于F
∴∠AFD=∠BED=90°,∠ADF+∠BDE=90°,∠ADF+∠FAD=90°
∴∠BDE=∠FAD
△AFD≌△DEB(AAS),
设DF=BE=a,
∵B(0,2),A(﹣6,﹣1),
∴OE=a+2=GF,DE=6﹣a,AF=a+3,
∵AF=DE,
∴a+3=6﹣a,
解得a=![]() ,
,
∴D(![]() ,
,![]() ),
),
设直线AD的解析式为y=k'x+b,则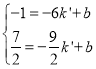 ,
,
解得![]() ,
,
∴y=3x+17,
∵A(﹣6,﹣1)在反比例函数![]() 的图象上,
的图象上,
∴k=6,即y=![]() ,
,
解方程组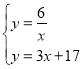 ,可得
,可得![]() 或
或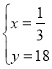 ,
,
∴点C的坐标为(![]() ,18),
,18),
故答案为:(![]() ,18).
,18).

【题目】某商店分两次购进![]() 、
、![]() 两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
两种商品进行销售,两次购进同一种商品的进价相同,具体情况如下表所示:
购进数量(件) | 购进所需费用 (元) | ||
A | B | ||
第一次 | 20 | 50 | 4100 |
第二次 | 30 | 40 | 3700 |
(1)求![]() 、
、![]() 两种商品每件的进价分别是多少元?
两种商品每件的进价分别是多少元?
(2)商场决定![]() 商品以每件50元出售,
商品以每件50元出售,![]() 商品以每件
商品以每件![]() 元出售.为满足市场需求,需购进
元出售.为满足市场需求,需购进![]() 、
、![]() 两种商品共
两种商品共![]() 件,且
件,且![]() 商品的数量不少于
商品的数量不少于![]() 商品数量的
商品数量的![]() 倍,请你求出获利最大的进货方案,并确定最大利润.
倍,请你求出获利最大的进货方案,并确定最大利润.