题目内容
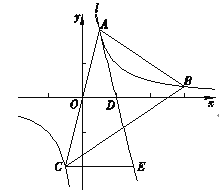
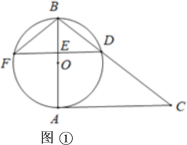
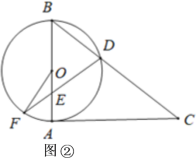
【题目】如图,在![]() 中,
中,![]() ,
,![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,将
,将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 上.
上.
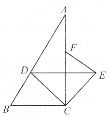
(1)![]() 旋转的度数为______
旋转的度数为______![]() ;
;
(2)连结![]() ,判断
,判断![]() 与
与![]() 的位置关系,并说明理由.
的位置关系,并说明理由.
【答案】(1)90;(2)DE∥BC,见解析
【解析】
(1)根据旋转的性质即可求得旋转角的度数;
(2)先利求得∠DCE=∠BCF=90°,CD=CE,可得△CDE为等腰直角三角形,即∠CDE=45°,再根据角平分线定义得到∠BCD=45°,则∠CDE=∠BCD,然后根据平行线的判定定理即可说明.
解:(1)解:∵将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上,
∴∠BCF=90°,即旋转角为90°;
故答案为90°.
(2)![]() ,理由如下:
,理由如下:
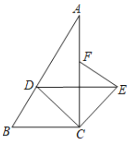
∵将![]() 绕点
绕点![]() 顺时针旋转到
顺时针旋转到![]() 的位置,点
的位置,点![]() 在
在![]() 上,
上,
∴![]() ,
,![]() ,
,
∴![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,
∵![]() 平分
平分![]() 交
交![]() 于点
于点![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() .
.

练习册系列答案
 初中暑期衔接系列答案
初中暑期衔接系列答案
相关题目
【题目】某印刷厂的打印机每5年需淘汰一批旧打印机并购买新机,买新机时,同时购买墨盒,每盒150元,每台新机最多可配买24盒;若非同时配买,则每盒需220元.
公司根据以往的记录,十台打印机正常工作五年消耗墨盒数如表:
消耗墨盒数 | 22 | 23 | 24 | 25 |
打印机台数 | 1 | 4 | 4 | 1 |
(1)以这十台打印机消耗墨盒数为样本,估计“一年该款打印机正常工作5年消耗的墨盒数不大于24”的概率;
(2)试以这10台打印机5年消耗的墨盒数的平均数作为决策依据,说明购买10台该款打印机时,每台应统一配买23盒墨还是24盒墨更合算?