题目内容
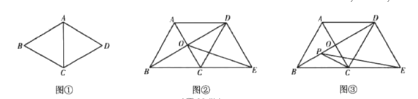
【题目】已知AB是⊙O的直径,AC是⊙O的切线,∠ABC=52°,BC交⊙O于点D,E是AB上一点,延长DE交⊙O于点F.
(Ⅰ)如图①,连接BF,求∠C和∠DFB的大小;
(Ⅱ)如图②,当DB=DE时,求∠OFD的大小.
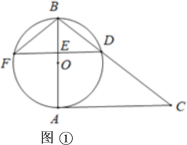
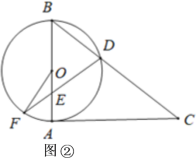
【答案】(Ⅰ)∠C=38°;∠DFB=38°;(Ⅱ)∠F=24°.
【解析】
(1)连接AD,利用切线的性质得出∠BAC=90°,从而得出∠C的度数;利用![]() 是⊙
是⊙![]() 的直径,得∠ADB=90°,从而得出∠DAB的度数,进而得出
的直径,得∠ADB=90°,从而得出∠DAB的度数,进而得出![]() 的度数;
的度数;
(2)连接OD,利用∠BED=∠B =52°,得出∠BDE的度数,利用OB=OD得出∠BDO的度数,从而得出∠ODF的度数,进而得出∠F的度数.
解:(Ⅰ)如图,连接AD.
∵ AC是⊙![]() 的切线,
的切线,![]() 是⊙
是⊙![]() 的直径,
的直径,
∴ AB⊥AC,即∠BAC=90°.
∵∠ABC=52° ,
∴∠C=90°-∠ABC=90°-52°=38°.
由![]() 是⊙
是⊙![]() 的直径,得∠ADB=90°.
的直径,得∠ADB=90°.
∴∠DAB=90°-∠ABC=90°-52°=38°.
∵![]()
∴![]() =∠DAB=38°.
=∠DAB=38°.
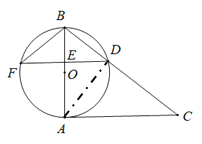
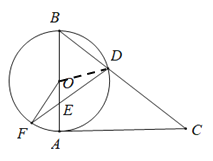
(Ⅱ)如图,连接OD.
在△BDE中,DB=DE,∠B=52°,
∴∠BED=∠B =52°,
∴∠BDE=180°-∠BED-∠B=76°.
又在△BOD中,OB=OD,∴∠BDO=∠B=52°,
∴ ∠ODF=76°-52°=24°.
∵ OD=OF,
∴∠F=∠ODF=24°.

练习册系列答案
相关题目