题目内容
【题目】已知抛物线y=x2+bx+c与x轴交于点A(4,﹣5).
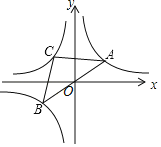
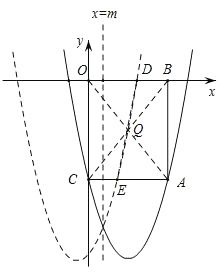
(1)如图,过点A分别向x轴、y轴作垂线,垂足分别为B、C,得到矩形ABOC,且抛物线经过点C.
①求抛物线的解析式.
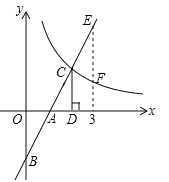
②将抛物线沿直线x=m(2>m>0)翻折,分别交线段OB、AC于D,E两点.若直线DE刚好平分矩形ABOC的面积,求m的值.
(2)将抛物线旋转180°,使点A的对应点为A1(m﹣2,n﹣4),其中m≤2.若旋转后的抛物线仍然经过点A,求旋转后的抛物线顶点所能达到最低点时的坐标.

【答案】(1)①y=x2﹣4x﹣5,②![]() ;(2)(2,﹣1)
;(2)(2,﹣1)
【解析】
(1)①由矩形的性质确定点C的坐标,将点C、A的坐标代入y=x2+bx+c即可求出抛物线的解析式;
②求出抛物线y=x2﹣4x﹣5的对称轴,求出翻折后的抛物线的对称轴,可写出翻折后的解析式,求出D,E两点坐标,因为直线DE刚好平分矩形ABOC的面积,则必过矩形对角线的交点Q(2,﹣![]() ),则可列出关于m的方程,即可求出m的值;
),则可列出关于m的方程,即可求出m的值;
(2)由点A、A1的坐标可求出旋转中心的坐标,进一步推出原顶点的对称点,可写出旋转后的抛物线解析式,因为旋转后的抛物线仍然经过点A,将点A的坐标代入旋转后的解析式,可得关于m、n的等式,将m=2代入,可求出n的值,即可写出旋转后的抛物线顶点所能达到最低点时的坐标.
解:(1)①∵点A(4,﹣5),且四边形ABOC为矩形,
∴C(0,﹣5),
∴抛物线的解析式为y=x2+bx﹣5,
将点A(4,﹣5)代入y=x2+bx﹣5,
得,b=﹣4,
∴抛物线的解析式为y=x2﹣4x﹣5;
②在抛物线y=x2﹣4x﹣5中,
对称轴为直线x=﹣![]() =2,
=2,
∵抛物线y=x2﹣4x﹣5沿直线x=m(2>m>0)翻折,
∴设翻折后的抛物线对称轴为直线x=n,
∴![]() =m,
=m,
∴n=2m﹣2,
∴翻折后的抛物线为y=[x﹣(2m﹣2)]2﹣9,
在y=[x﹣(2m﹣2)]2﹣9中,当y=0时,x1=2m+1,x2=2m﹣5;当y=﹣5时,x1=2m,x2=2m﹣4;
∵如下图,抛物线y=[x﹣(2m﹣2)]2﹣9分别交线段OB、AC于D,E两点,
∴D(2m+1,0),E(2m,﹣5),
∵直线DE刚好平分矩形ABOC的面积,
∴必过矩形对角线的交点Q(2,﹣![]() ),
),
即![]() =2,
=2,
∴m=![]() ;
;
(2)∵将抛物线旋转180°,使点A的对应点为A1(m﹣2,n﹣4),其中m≤2,
∵A(4,﹣5),
∴旋转中心为(![]() ,
,![]() ),
),
∴原顶点的对称点为(m,n),
∴旋转后的抛物线为y=﹣(x﹣m)2+n,
∵旋转后的抛物线仍然经过点A,
∴﹣5=﹣(4﹣m)2+n,
∵m≤2,
∴当m=2时,n=﹣1,
∵旋转后抛物线开口向下,
∴旋转后的抛物线顶点所能达到最低点时的坐标(2,﹣1).

【题目】中华文明,源远流长,中华汉字,寓意深广.为传承中华优秀传统文化,某中学德育处组织了一次全校2000名学生参加的“汉字听写”大赛.为了解本次大赛的成绩,学校德育处随机抽取了其中200名学生的成绩作为样本进行统计,制成如下不完整的统计图表:
成绩x(分)分数段 | 频数(人) | 频率 |
50≤x<60 | 10 | 0.05 |
60≤x<70 | 30 | 0.15 |
70≤x<80 | 40 | 0.2 |
80≤x<90 | m | 0.35 |
90≤x<100 | 50 | n |
频数分布直方图
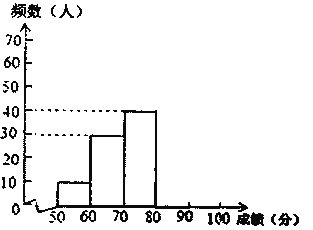
根据所给的信息,回答下列问题:
(1)m=________;n=________;
(2)补全频数分布直方图;
(3)这200名学生成绩的中位数会落在________分数段;
(4)若成绩在90分以上(包括90分)为“优”等,请你估计该校参加本次比赛的2000名学生中成绩是“优”等的约有多少人?