题目内容
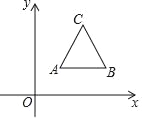
【题目】已知点A在x轴负半轴上,点B在y轴正半轴上,线段OB的长是方程x2﹣2x﹣8=0的解,tan∠BAO=![]() .
.
(1)求点A的坐标;
(2)点E在y轴负半轴上,直线EC⊥AB,交线段AB于点C,交x轴于点D,S△DOE=16.若反比例函数y=![]() 的图象经过点C,求k的值;
的图象经过点C,求k的值;
(3)在(2)条件下,点M是DO中点,点N,P,Q在直线BD或y轴上,是否存在点P,使四边形MNPQ是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.

【答案】(1)(-8,0)(2)k=-![]() (3)(﹣1,3)或(0,2)或(0,6)或(2,6)
(3)(﹣1,3)或(0,2)或(0,6)或(2,6)
【解析】
(1)解方程求出OB的长,解直角三角形求出OA即可解决问题;
(2)求出直线DE、AB的解析式,构建方程组求出点C坐标即可;
(3)分四种情形分别求解即可解决问题;
(1)∵线段OB的长是方程x2﹣2x﹣8=0的解,
∴OB=4,
在Rt△AOB中,tan∠BAO=![]() ,
,
∴OA=8,
∴A(﹣8,0).
(2)∵EC⊥AB,
∴∠ACD=∠AOB=∠DOE=90°,
∴∠OAB+∠ADC=90°,∠DEO+∠ODE=90°,
∵∠ADC=∠ODE,
∴∠OAB=∠DEO,
∴△AOB∽△EOD,
∴![]() ,
,
∴OE:OD=OA:OB=2,设OD=m,则OE=2m,
∵![]() m2m=16,
m2m=16,
∴m=4或﹣4(舍弃),
∴D(﹣4,0),E(0,﹣8),
∴直线DE的解析式为y=﹣2x﹣8,
∵A(﹣8,0),B(0,4),
∴直线AB的解析式为y=![]() x+4,
x+4,
由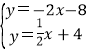 ,解得
,解得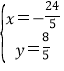 ,
,
∴C(![]() ,
,![]() ),
),
∵若反比例函数y=![]() 的图象经过点C,
的图象经过点C,
∴k=﹣![]() .
.
(3)如图1中,当四边形MNPQ是矩形时,∵OD=OB=4,
∴∠OBD=∠ODB=45°,
∴∠PNB=∠ONM=45°,
∴OM=DM=ON=2,
∴BN=2,PB=PN=![]() ,
,
∴P(﹣1,3).
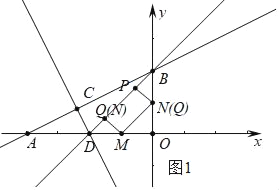
如图2中,当四边形MNPQ是矩形时(点N与原点重合),易证△DMQ是等腰直角三角形,OP=MQ=DM=2,P(0,2);
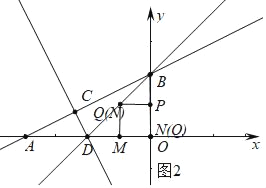
如图3中,当四边形MNPQ是矩形时,设PM交BD于R,易知R(﹣1,3),可得P(0,6)
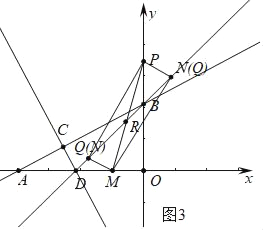
如图4中,当四边形MNPQ是矩形时,设PM交y轴于R,易知PR=MR,可得P(2,6).
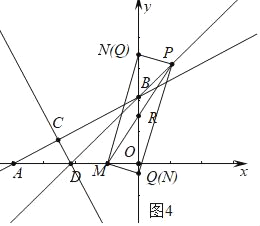
综上所述,满足条件的点P坐标为(﹣1,3)或(0,2)或(0,6)或(2,6);

 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案 冲刺100分单元优化练考卷系列答案
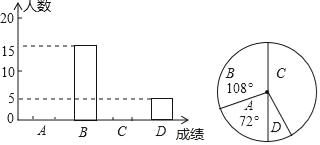
冲刺100分单元优化练考卷系列答案【题目】某校九年级数学测试后,为了解学生学习情况,随机抽取了九年级部分学生的数学成绩进行统计,得到相关的统计图表如下.
成绩/分 | 120﹣111 | 110﹣101 | 100﹣91 | 90以下 |
成绩等级 | A | B | C | D |
请根据以上信息解答下列问题:
(1)这次统计共抽取了 名学生的数学成绩,补全频数分布直方图;
(2)若该校九年级有1000名学生,请据此估计该校九年级此次数学成绩在B等级以上(含B等级)的学生有多少人?
(3)根据学习中存在的问题,通过一段时间的针对性复习与训练,若A等级学生数可提高40%,B等级学生数可提高10%,请估计经过训练后九年级数学成绩在B等级以上(含B等级)的学生可达多少人?