题目内容
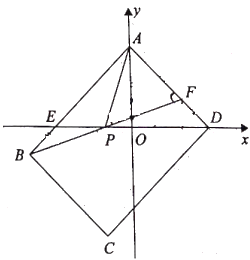
【题目】如图,在平面直角坐标系xOy中,点![]() ,
, ![]() 在反比例函数
在反比例函数![]() (m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点
(m为常数)的图象上,连接AO并延长与图象的另一支有另一个交点为点C,过点A的直线l与x轴的交点为点![]() ,过点C作CE∥x轴交直线l于点E.
,过点C作CE∥x轴交直线l于点E.
(1)求m的值,并求直线l对应的函数解析式;
(2)求点E的坐标;
(3)过点B作射线BN∥x轴,与AE交于点M (补全图形),求证: ![]()
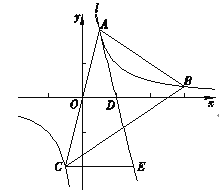
【答案】(1)m=1;y=-4x+4;(2)E(![]() ,-2);(3)证明见解析.
,-2);(3)证明见解析.
【解析】试题分析:(1)将点A(![]() ,2)代入
,2)代入![]() 求出m的值,再将A(
求出m的值,再将A(![]() ,2),D(1,0)分别代入y=kx+b,求出k、b的值;
,2),D(1,0)分别代入y=kx+b,求出k、b的值;
(2)由反比例函数图象的中心对称性可知点C的坐标为C(﹣![]() ,﹣2),由yE=yC求出E点坐标.
,﹣2),由yE=yC求出E点坐标.
(3)作AF⊥BN于点G,与射线BN交于点G,作CH⊥BN 于点H,由于点B(3,n)在反比例函数图象上,求出n=![]() ,在Rt△ABG中、Rt△BCH中,求出tan∠ABH和tan∠CBH的值即可.
,在Rt△ABG中、Rt△BCH中,求出tan∠ABH和tan∠CBH的值即可.
试题解析:解:(1)∵点A(![]() ,2)在反比例函数
,2)在反比例函数![]() (m为常数)的图象上,∴m=
(m为常数)的图象上,∴m=![]() ×2=1,∴反比例函数
×2=1,∴反比例函数![]() (m为常数)对应的函数表达式是
(m为常数)对应的函数表达式是![]() .
.
设直线l对应的函数表达式为y=kx+b(k,b为常数,k≠0).
∵直线l经过点A(![]() ,2),D(1,0),∴
,2),D(1,0),∴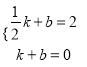 ,解得:
,解得: ![]() ,∴直线l对应的函数表达式为y=﹣4x+4.
,∴直线l对应的函数表达式为y=﹣4x+4.
(2)由反比例函数图象的中心对称性可知点C的坐标为C(﹣![]() ,﹣2).
,﹣2).
∵CE∥x轴交直线l于点E,∴yE=yC,∴点E的坐标为E(![]() ,﹣2).
,﹣2).
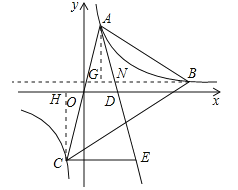
(3)如图,作AF⊥BN于点G,与射线BN交于点G,作CH⊥BN 于点H,∵点B(3,n)在反比例函数图象上,∴n=![]() ,∴B(3,
,∴B(3, ![]() ),G(
),G(![]() ,
, ![]() ),H(﹣
),H(﹣![]() ,
, ![]() ).
).
在Rt△ABG中,tan∠ABH= ,在Rt△BCH中,tan∠CBH=
,在Rt△BCH中,tan∠CBH= ,∴tan∠ABN=tan∠CBN.
,∴tan∠ABN=tan∠CBN.

【题目】某公司需招聘一名员工,对应聘者甲、乙、丙从笔试、面试、体能三个方面进行量化考核.甲、乙、丙各项得分如下表:
笔 试 | 面 试 | 体 能 | |
甲 | 85 | 80 | 75 |
乙 | 80 | 90 | 73 |
丙 | 83 | 79 | 90 |
(1)根据三项得分的平均分,从高到低确定三名应聘者的排名顺序.
(2)该公司规定:笔试,面试、体能得分分别不得低于80分,80分,70分,并按60%,30%,10%的比例计入总分(不计其他因素条件),请你说明谁将被录用.