题目内容
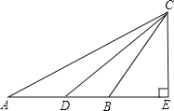
【题目】如图,在△ABC和△ABD中,∠BAC=∠ABD=90°,点E为AD边上的一点,且AC=AE,连接CE交AB于点G,过点A作AF⊥AD交CE于点F.
(1)求证:△AGE≌△AFC;
(2)若AB=AC,求证:AD=AF+BD.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
(1)由AF⊥AD,∠CAB=90°,可得∠CAF=∠EAG,由AC=AE,可得∠ACF=∠AEG,根据AAS即可证明结论;
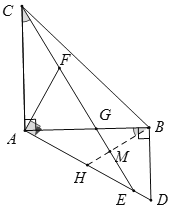
(2)如图,在AD上截取AH=AE,交CE于点M,证明△CAF≌△BAH,从而可得∠ABH=∠ACF,继而可得∠MGB+∠ABH=90°,从而可得∠MHE+∠HEM=90°,再根据∠ACF=∠HEM,∠ABH+∠HBD=90°,可得到∠MHE=∠HBD,从而可得HD=BD,再根据AD=AH+DH,即可求得答案.
(1)∵AF⊥AD,
∴∠FAE=90°,
∵∠CAB=90°,
∴∠CAB-∠FAB=∠FAE-∠FAB,
即∠CAF=∠EAG,
∵AC=AE,
∴∠ACF=∠AEG,
∴△AGE≌△AFC(AAS);
(2)如图,在AD上截取AH=AE,交CE于点M,
又∵∠CAF=∠BAH,AC=BC,
∴△CAF≌△BAH(SAS),
∴∠ABH=∠ACF,
∵∠CGA=∠MGB,∠ACF+∠CGA=90°,
∴∠MGB+∠ABH=90°,
∴∠BMG=90°,
∴∠HME=∠BMG=90°,
∴∠MHE+∠HEM=90°,
又∵∠ACF=∠HEM,∠ABH+∠HBD=90°,
∴∠MHE=∠HBD,
∴HD=BD,
∵AD=AH+DH,
∴AD=AF+BD.

练习册系列答案
相关题目