��Ŀ����
����Ŀ����ADE�У�AE=AD����EAD=90�㣮


��1����ͼ��1������EC��DB�ֱ�ƽ�֡�AED����ADE����AD��AE�ڵ�C��B������BC�������ж�AB��AC�Ƿ���ȣ���˵�����ɣ�
��2����ADE��λ�ñ��ֲ��䣬����1���еġ�ABC�Ƶ�A��ʱ����ת��ͼ
��2����λ�ã�CD��BE�ཻ��O�������ж��߶�BE��CD��λ�ù�ϵ��������ϵ����˵�����ɣ�
��3���ڣ�2���������£���CD=6�������ı���CEDB�������
���𰸡���1�����ɼ���������2�����ɼ���������3��18.
����������������1������֪�á�AEC=��ADB��AE=AD����A=��A�����á�ASA��֤����AEC�ա�ADB���ɣ���2��BE=CD��BE��CD������ת�����ʿ�֤��AEB�ա�ADC���Ӷ��ɵ�BE=CD�������ýǵ���ȹ�ϵ�������ϵ֤��BE��CD����3������BE��CD��BE=CD=6�����ı��εĶԽ����ഹֱʱ���ı��ε�������ڶԽ�����һ�룮
���������
(1)AB=AC.
�������£�
��EC��DB�ֱ�ƽ�֡�AED����ADE
���AEC=![]() ��AED,��ADB=
��AED,��ADB=![]() ��ADE
��ADE
�ߡ�AED=��ADE
���AEC=��ADB
�ڡ�AEC�͡�ADB�У�
��AEC=��ADB��AE=AD����A=��A
���AEC�ա�ADB
��AB=AC��
(2)BE=CD��BE��CD.
�������£�
�ߡ�EAD=��BAC
���EAB=��DAC
�ڡ�AEB�͡�ADC�У�
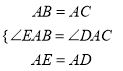 ��
��
���AEB�ա�ADC(SAS)
��EB=CD
���AEB=��ADC
�ߡ�AEB+��DEB+��ADE=90��
���ADC+��DEB+��ADE=90��
�ߡ�ADC+��DEB+��ADE+��DOE=180��
���DOE=90��
��BE��CD��
(3)�ı���CEDB�����=![]() ��BE��CD=
��BE��CD=![]()
![]() =18.
=18.

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�