题目内容
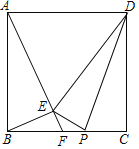
【题目】如图1,在正方形ABCD中,M是AD的中点,点E是边AB上的一个动点,连接EM并延长交射线CD于点F,过点M作EF的垂线交射线BC于点G,连结EG、FG.

![]() 求证:
求证:![]() ≌
≌![]() ;
;![]() .
.
![]() 在点E的运动过程中,探究:
在点E的运动过程中,探究:
![]() 的值是否发生变化?若不变,求出这个值;
的值是否发生变化?若不变,求出这个值;
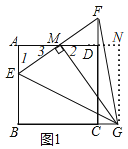
![]() 如图2,把正方形ABCD改为矩形
如图2,把正方形ABCD改为矩形![]() ,
,![]() ,
,![]() ,其他条件不变,当
,其他条件不变,当![]() 为等边三角形时,试求k的值.
为等边三角形时,试求k的值.
【答案】![]() 证明见解析;
证明见解析;![]() 证明见解析;
证明见解析;![]() 的值不变,值为2;
的值不变,值为2;![]() .
.
【解析】
(1)![]() 根据正方形性质得
根据正方形性质得![]() .
.![]() .又
.又![]() ,可证
,可证![]() ≌
≌![]() ;
;![]() ;(2)
;(2)![]() 的值不变.如图1,过点G作
的值不变.如图1,过点G作![]() ,垂足为点N,由矩形性质,证
,垂足为点N,由矩形性质,证![]() ∽
∽![]() ,得
,得![]() ,所以,
,所以,![]() 为定值不变;
为定值不变;![]() 如图2,过点G作
如图2,过点G作![]() ,垂足为点N,由四边形ABGN是矩形.
,垂足为点N,由四边形ABGN是矩形.![]() .由等边三角形性质,得
.由等边三角形性质,得![]() ,同
,同![]() 的方法得,
的方法得,![]() ∽
∽![]() ,
,![]() ,
,![]() 是AD的中点,
是AD的中点,![]() ,可求得k.
,可求得k.
![]() 四边形ABCD是正方形,
四边形ABCD是正方形,
![]() .
.
![]() 是AD的中点,
是AD的中点,
![]() .
.
又![]() ,
,
![]() ≌
≌![]() ;
;
![]() 由
由![]() ≌
≌![]() ,
,
![]() .
.
![]() ,
,
![]() ;
;
![]() 的值不变.
的值不变.
如图1,过点G作![]() ,垂足为点N,
,垂足为点N,
则四边形ABGN是矩形.
![]() .
.
![]() ,
,
![]() .
.
在![]() 中,
中,![]() ,
,
![]() .
.
![]() .
.
![]() ∽
∽![]() ,
,
![]() ,
,
![]() 为定值不变;
为定值不变;
![]() 如图2,过点G作
如图2,过点G作![]() ,垂足为点N,
,垂足为点N,
则四边形ABGN是矩形.
![]() .
.
若![]() 是等边三角形,则
是等边三角形,则![]() ,
,
同![]() 的方法得,
的方法得,![]() ∽
∽![]() ,
,
![]() ,
,
![]() 是AD的中点,
是AD的中点,
![]() ,
,
![]() .
.

练习册系列答案
相关题目