题目内容
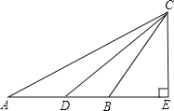
【题目】在△ABC中,∠A=∠ACB,CD是△ABC的角平分线,CE是△ABC的高.
(1)试说明∠CDB=3∠DCB.
(2)若∠DCE=48°,求∠ACB的度数.
【答案】(1)见解析;(2)28°.
【解析】
(1)根据题意设∠A为2x,则∠ACB=2x,∠ACD=x,由三角形的外角定理得出∠CDB=∠A+∠ACD=3x,即可得出结论;
(2)求出∠CDB=42°,由(1)得出∠DCB=14°得出∠ACB=28°即可.
解:(1)证明:由题意设∠A=2x,
∴∠A=∠ACB=2x,
∵CD是∠ACB的角平分线,
∠ACD=∠DCB=x,
∴由三角形的外角定理可知:
∠CDB=∠A+∠ACD=2x+x=3x,
∴∠CDB=3∠DCB.
(2)∵CE是△ABC的高,
∴∠E=90°,
∵∠DCE=48°,
∴∠CDB=∠E-∠DCE=90°- 48°= 42°,
由(1)可知∠CDB=3∠DCB=42°,
∴∠DCB=14°
∴∠ACB=2∠DCB=2×14°=28°.
故答案为:28°.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案
相关题目






