Question

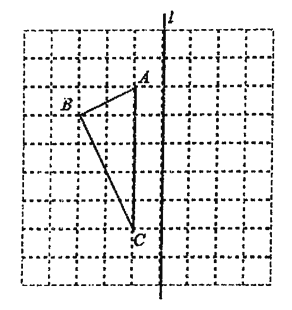
【题目】如图，在△ABC中，AB＝AC，D为三角形内一点，且△DBC为等边三角形．

（1）求证：直线AD垂直平分BC；

（2）以AB为一边，在AB的右侧画等边△ABE，连接DE，试判断以DA，DB，DE三条线段是否能构成直角三角形？请说明理由．

Answer 1

【答案】（1）见解析；（2）能构成直角三角形，理由见解析.

【解析】

(1)由AB=AC确定点A在线段BC的垂直平分线上，再由等边三角形△DBC知DB=DC，即可确定直线AD垂直平分BC；（2）连接CE，利用三角形全等证明AD=CE，再依据DB=DC，将三条边转化为同一个三角形的三条边，再求得∠DCE=900即可判断.

证明：（1）∵△DBC为等边三角形，

∴DB＝DC，

∴D在BC的垂直平分线上，

∵AB＝AC，

∴A在BC的垂直平分线上，

∴直线AD垂直平分BC；

（2）以DA，DB，DE三条线段能构成直角三角形；

连接CE，

∵∠ABE=∠DBC=60°，

∠ABE﹣∠DBE＝∠DBC﹣∠DBE，

∴∠ABD＝∠EBC，

在△EBC和△ABD中，，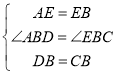

∴△EBC≌△ABD，

∴∠BCE＝∠ADB，AD＝CE，

在△ADB和△ADC中， ，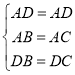

∴△ADB≌△ADC，

∴∠ADB＝∠ADC，

∴∠ADB＝（360°﹣∠BCD）＝150°，

∴∠BCE＝∠BDA＝150°，

∴∠DCE＝∠BCE﹣∠BCD＝150°﹣60°＝90°，

∵CE＝DA，DC＝DB，

∴以DA，DB，DE三条线段能构成直角三角形.-