��Ŀ����
����Ŀ����ͼ��������y=ax2+bx��a��0������E��10��0��������ABCD�ı�AB���߶�OE�ϣ���A�ڵ�B����ߣ�����C��D���������ϣ���A��t��0������t=2ʱ��AD=4��
��1���������ߵĺ�������ʽ��
��2����tΪ��ֵʱ������ABCD���ܳ������ֵ�����ֵ�Ƕ��٣�
��3������t=2ʱ�ľ���ABCD����������ƽ�������ߣ���ƽ�ƺ������������εı�����������G��H����ֱ��GHƽ�־��ε����ʱ����������ƽ�Ƶľ��룮

���𰸡���1�������ߵĺ�������ʽΪy=��![]() x2+
x2+![]() x����2����t=1ʱ������ABCD���ܳ������ֵ�����ֵΪ
x����2����t=1ʱ������ABCD���ܳ������ֵ�����ֵΪ![]() ����3������������ƽ�Ƶľ�����4����λ��
����3������������ƽ�Ƶľ�����4����λ��
����������1���ɵ�E�������������ߵĽ���ʽ���ٰѵ�D�����꣨2��4���������ɵã�
��2���������ߵĶԳ��Ե�BE=OA=t���ݴ�֪AB=10-2t������x=tʱAD=-![]() t2+
t2+![]() t�����ݾ��ε��ܳ���ʽ�г���������ʽ���䷽�ɶ���ʽ���ɵã�
t�����ݾ��ε��ܳ���ʽ�г���������ʽ���䷽�ɶ���ʽ���ɵã�
��3����t=2�ó���A��B��C��D���Խ��߽���P�����꣬��ֱ��GHƽ�־��ε����ֱ֪��GH�ع���P������AB��CD֪�߶�ODƽ�ƺ�õ����߶���GH�����߶�OD���е�Qƽ�ƺ�Ķ�Ӧ����P֪PQ����OBD��λ�ߣ��ݴ˿ɵã�
��1���������߽���ʽΪy=ax��x-10����
�ߵ�t=2ʱ��AD=4��
���D��������2��4����
�ཫ��D����������ʽ��-16a=4��
��ã�a=-![]() ��
��
�����ߵĺ�������ʽΪy=-![]() x2+
x2+![]() x��
x��
��2���������ߵĶԳ��Ե�BE=OA=t��
��AB=10-2t��
��x=tʱ��AD=-![]() t2+
t2+![]() t��
t��
�����ABCD���ܳ�=2��AB+AD��
=2[��10-2t��+��-![]() t2+
t2+![]() t��]
t��]
=-![]() t2+t+20
t2+t+20
=-![]() ��t-1��2+
��t-1��2+![]() ��
��
��-![]() ��0��
��0��
�൱t=1ʱ������ABCD���ܳ������ֵ�����ֵΪ![]() ��
��
��3����ͼ��
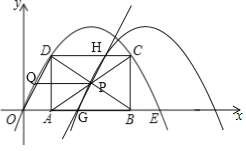
��t=2ʱ����A��B��C��D������ֱ�Ϊ��2��0������8��0������8��4������2��4����
�����ABCD�Խ��ߵĽ���P������Ϊ��5��2����
��ƽ�ƺ�������߹���Aʱ����H������Ϊ��4��4������ʱGH���ܽ��������ƽ�֣�
��ƽ�ƺ�������߹���Cʱ����G������Ϊ��6��0������ʱGHҲ���ܽ��������ƽ�֣�
�൱G��H����һ�������߶�AD��BC��ʱ��ֱ��GH�����ܽ����ε����ƽ�֣�
����G��H�ֱ������߶�AB��DC��ʱ��ֱ��GH����P��ƽ�־���ABCD�������
��AB��CD��
���߶�ODƽ�ƺ�õ����߶�GH��
���߶�OD���е�Qƽ�ƺ�Ķ�Ӧ����P��
����OBD�У�PQ����λ�ߣ�
��PQ=![]() OB=4��
OB=4��
��������������ƽ�Ƶľ�����4����λ��

����Ŀ��(10�֣�ѧУ��֯ѧ���μ��ۺ�ʵ��������Dz�����ij��Ʒ���˶�Ь�����۹�������֪���˶�Ьÿ˫�Ľ���Ϊ120Ԫ��ΪѰ����ʵ����ۼ۸������4�������������������±���ʾ��
��1�� | ��2�� | ��3�� | ��4�� | |
�ۼ�x��Ԫ/˫�� | 150 | 200 | 250 | 300 |
������y��˫�� | 40 | 30 | 24 | 20 |
��1���۲�������ݣ�x��y����ʲô������ϵ����������������ϵʽ��
��2�����̳��ƻ�ÿ�����������Ϊ3000Ԫ�����䵥�۶�Ϊ����Ԫ��