��Ŀ����
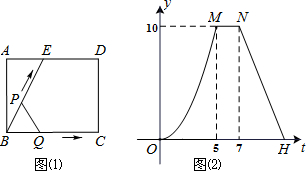
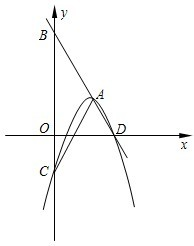
��ͼ��1����ʾ��EΪ����ABCD�ı�AD��һ�㣬����P��Qͬʱ�ӵ�B��������P������BE-ED-DC�˶�����Cʱֹͣ����Q��BC�˶�����Cʱֹͣ�������˶����ٶȶ���1cm/�룮��P��Qͬʱ����t��ʱ����BPQ�����Ϊycm2����֪y��t�ĺ�����ϵͼ����ͼ��2��������OMΪ�����ߵ�һ���֣��������н��۴�����ǣ�������
| A��AD=BE=5cm | ||
B��cos��ABE=
| ||
C����0��t��5ʱ��y=
| ||
D����t=
|

����ͼ��2���ɵã�����P�����Eʱ��Q�����C��
�ߵ�P��Q���˶����ٶȶ���1cm/�룬
��BC=BE=5��
��AD=BE=5����Aѡ����ȷ��
�֡ߴ�M��N�ı仯��2��
��ED=2��
��AE=AD-ED=5-2=3��
��Rt��ABE��AB=
=
=4��
��cos��ABE=
=
����Bѡ�����
��ͼ��1������P��PF��BC�ڵ�F��
��AD��BC��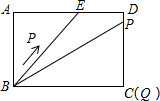
���AEB=��PBF��
��sin��PBF=sin��AEB=
=
��
��PF=PBsin��PBF=
t��
�൱0��t��5ʱ��y=
BQ•PF=
t•
t=
t2����Cѡ����ȷ��
��t=
��ʱ����P��CD�ϣ���ʱ��PD=
-BE-ED=
-5-2=
��
PQ=CD-PD=4-
=
��
��
=
��
=
��
��
=
��
�֡ߡ�A=��Q=90�㣬
���ABE����QBP����Dѡ����ȷ��
��ѡB��
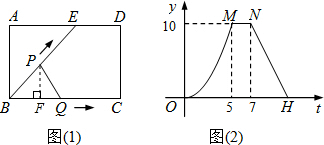
�ߵ�P��Q���˶����ٶȶ���1cm/�룬
��BC=BE=5��
��AD=BE=5����Aѡ����ȷ��
�֡ߴ�M��N�ı仯��2��
��ED=2��
��AE=AD-ED=5-2=3��
��Rt��ABE��AB=
| BE2-AE2 |
| 52-32 |
��cos��ABE=
| AB |
| BE |
| 4 |
| 5 |
��ͼ��1������P��PF��BC�ڵ�F��
��AD��BC��

���AEB=��PBF��
��sin��PBF=sin��AEB=
| AB |
| BE |
| 4 |
| 5 |
��PF=PBsin��PBF=
| 4 |
| 5 |
�൱0��t��5ʱ��y=
| 1 |
| 2 |
| 1 |
| 2 |
| 4 |
| 5 |
| 2 |
| 5 |
��t=
| 29 |
| 4 |
| 29 |
| 4 |
| 29 |
| 4 |
| 1 |
| 4 |
PQ=CD-PD=4-
| 1 |
| 4 |
| 15 |
| 4 |
��
| AB |
| AE |
| 4 |
| 3 |
| BQ |
| PQ |
| 4 |
| 3 |
��
| AB |
| AE |
| BQ |
| PQ |
�֡ߡ�A=��Q=90�㣬
���ABE����QBP����Dѡ����ȷ��
��ѡB��


��ϰ��ϵ�д�
�����Ŀ

 x2���ң�x1+1����x2+1��=5
x2���ң�x1+1����x2+1��=5