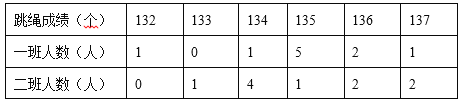
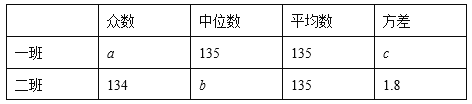
题目内容
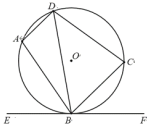
【题目】如图，四边形ABCD内接于⊙O，AD∥BC，直线EF是⊙O的切线，B是切点．若∠C＝80°，∠ADB＝54°，则∠CBF＝____°．
【答案】46°
【解析】
连接OB，OC，根据切线的性质可知∠OBF=90°，根据AD∥BC，可得∠DBC=∠ADB＝54°，然后利用三角形内角和求得∠BDC=46°，然后利用同弧所对的圆心角是圆周角的2倍，求得∠BOC=92°，然后利用等腰三角形的性质求得∠OBC的度数，从而使问题得解.
解：连接OB，OC，
∵直线EF是⊙O的切线，B是切点
∴∠OBF=90°
∵AD∥BC
∴∠DBC=∠ADB＝54°
又∵∠DCB＝80°
∴∠BDC=180°-∠DBC -∠DCB=46°
∴∠BOC=2∠BDC =92°
又∵OB=OC
∴∠OBC=
∴∠CBF＝∠OBF-∠OBC=90-44=46°
故答案为：46°
练习册系列答案
相关题目
