题目内容
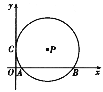
【题目】如图,⊙P与y轴相切于点C(0,3),与x轴相交于点A(1,0),B(9,0).直线y=kx-3恰好平分⊙P的面积,那么k的值是 ( )
A. ![]()
B. ![]()
C. ![]()
D. 2
【答案】A
【解析】
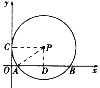
连接PC,PA,过点P作PD⊥AB于点D,根据切线的性质可知PC⊥y轴,故可得出四边形PDOC是矩形,所以PD=OC=3,再求出AB的长,由垂径定理可得出AD的长,故可得出OD的长,进而得出P点坐标,再把P点坐标代入直线y=kx-3即可得出结论.
连接PC,PA,过点P作PD⊥AB于点D,∵⊙P与y轴相切于点C(0,3),∴PC⊥y轴,∴四边形PDOC是矩形,∴PD=OC=3,∵A(1,0),B(9,0),∴AB=9-1=8,∴AD=![]() AB=
AB=![]() ×8=4,∴OD=AD+OA=4+1=5,∴P(5,3),∵直线y=kx-3恰好平分⊙P的面积,∴点P在直线y=kx-3上,∴3=5k-3,解得
×8=4,∴OD=AD+OA=4+1=5,∴P(5,3),∵直线y=kx-3恰好平分⊙P的面积,∴点P在直线y=kx-3上,∴3=5k-3,解得![]() .故选A.
.故选A.

练习册系列答案
相关题目